Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAT136

Assignment 2

Due: July 30 at 11:59pm

All solutions  should  be  written  or  typeset,  and  include  appropriate  details  and  explanations.   Please  upload your solutions to  Gradescope as a single PDF file.  When submitting on  Gradescope, please mark the location of each question  on your submission  by assigning pages to  corresponding  questions.

1.  The region bounded by the curves y = 2x and y = x2  is rotated around

a. the x-axis;

b. the y-axis;

c. the line y = −2.

Compute the volume of the resulting solid in each of the three cases.  Show your steps.

2.  The city of Mathville has a population density which depends solely on the radial distance to the centre of the city, which is marked with a statue of Euclid.  Such radial density is given by ρ(r) = 7000e −0.03r2  where r is the radius from Euclid’s statute.

(a)  Historically, Downtown Mathville is the circular region centred at Euclid’s statue with radius 4km. What is the population of Downtown Mathville?

(b)  For the purpose of understanding the Mathville suburbs, city officials want to understand how many people live in the annulus of width 2km immediately outside of Mathville Downtown.  This is the outer ring immediately after Mathville Downtown going as far as 2km away on any direction. Compute the population on this region.

(c)  Scienceland, the country where Mathville is, wants to reshape the electoral ridings before next year elections. They want the Mathville riding be circular, be centred at Euclid’s statue, and to include 500,000 people. What must be the radius of the new riding?

3.  Consider the Initial Value Problem (IVP) given by

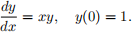
a.  Sketch the slope field of the differential equation for values of (x,y) in the square (−1, 1) × ( −1, 1). You can use digital graphing tool if needed; however, verify the slope field by computing the slope at, at least, two points.

b.  Use the Euler method to approximate the solution y(x) of the IVP at points x0  = 0, x1  = 0.1, x2  = 0.2, x3  = 0.3.  Show your steps.

c.  Find the exact solution of the IVP. Show your steps.

4. We studied the Lotka-Volterra model for predators and preys in class.  There are systems of differential equations that model the growth and decline of populations of two competing species, they usually compete for their food supply. Let’s see one!

Let us work in a small region in of the Caribbean sea:  Isla Paraiso.   Let x be the population  (in thousands) of the invasive lionfish that has become dominant in many places in the Caribbean, far from its natural Indo-Pacific waters.  Let y be the population (in hundreds) of the local blacktip sharks. They both compete for the little fish around Isla Paraiso.  The following system of differential equations models their populations:

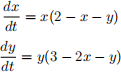
(a) What are the equilibrium solutions of the system?

(b) What is the differential equation satisfied by y(x)?

(c)  Draw the phase portrait of this system.

(d)  Explain why these equations make it mathematically possible, but extremely unlikely, for both species to survive.