Physics 122 Summer 2023 Practice Problems
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Physics 122 Summer 2023
Practice Problems
Practice problems are not for credit and will not be graded.
They will be helpful in preparation for the first exam on Wednesday, July 19.
Checklist for First Midterm
The list is not meant to be comprehensive but if you can do all of the following you should do very well on the exam.
✷ 1. Use a symmetry argument to determine the direction of the electric field.
✷ 2. Determine the direction of the electric field by breaking up the source into pairs of symmetrically placed charges.
✷ 3. Use Coulomb’s law to write a vector expression for the electric field due to a point charge. By vector expression I mean using unit vectors.
✷ 4. Use Coulomb’s law to write a vector expression for the electric field due to an infinites- imal segment of charge.
✷ 5. Use superposition to add the electric field vectors due to several point charges.
✷ 6. Use superposition and integration to determine the electric field of linear distributions of charges such as lines, rings and circular arcs.
✷ 7. For simple charge distributions be able to guess the form of the electric field at large and small distances.
✷ 8. Make simple approximations such as these.
 (1)
(1)
provided a ≫ b. In case of more complicated approximations we will supply you with necessary formulae.
✷ 9. Be able to determine the charge enclosed by a Gaussian surface.
✷ 10. Be able to evaluate the flux through a Gaussian surface. This involves being able to determine the direction of the outward normal unit vector n(ˆ) on the Gaussian surface; knowing that if the electric field lies in the plane of a surface, then the flux through that surface is zero; and knowing that ifn(ˆ) · E is constant over a surface, then the flux is just the area of that surface times the constant value of n(ˆ) · E(ˆ) .

Figure 1: Two positive charges.
1. Electrostatics of molecular hydrogen. A pair of charges, each with positive charge +q, are placed on the y-axis, symmetrically about the origin, separated by a distance 2a from each other, as shown in fig 1.
(a) [15 points] (i) What is the direction of the electric field at the point marked A in fig 1?
(ii) Determine the electric field at A. Give your answer in terms of q,ϵ0 ,x,a, i(ˆ) and j(ˆ).
(iii) What do you expect the electric field to be at large distances (for x ≫ a)? Explain briefly (one or two sentences). Does your answer of part (ii) reduce to the expected result?
Useful approximation:
 (2)
(2)
(b) [5 points] Suppose the two particles are protons in a hydrogen molecule. Calculate the force between the protons in Newtons. Useful data: Charge of proton, q = 1.6×10− 19 C. The
bond length of molecular hydrogen is 0.74A(˚) corresponding to the parameter a = 3.7×10− 11
m. 1/4πϵ0 = 9.0 × 109 N m2 /C2 .
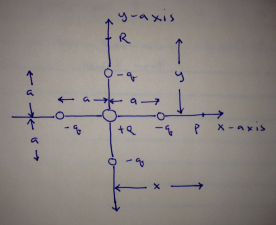
Figure 2: A complex ion.
2. Complex ion. A complex ion consists of a central cation of charge +Q surrounded by four “ligands” of charge −q as shown in the figure 2.
(a) In what direction do you expect the electric field to point at the points P and R shown in the figure?
(b) Let S be a point on the z-axis an elevation z above the central cation. In what direction do you expect the electric field to point at S?
(c) Determine the electric field at P. Give your answer in terms of Q,q,ϵ0 ,a,x and the unit
vectors i(ˆ), j(ˆ) and k(ˆ) .
(d) What electric field do you expect at P if x ≫ a? Does your result of part (c) simplify to the expected answer?
(e) Determine the electric field at S. Give your answer in terms of Q,q,ϵ0 ,a,z and the unit
vectors i(ˆ), j(ˆ) and k(ˆ) .
(f) What do you expect the electric field to be if S is far away from the complex ion, (i.e., z ≫ a)? Does your result of part (e) reduce to the expected result?
3. Charged line segment and junction. A charged line segment of length 2ℓ lies on the y-axis placed symmetrically about the origin as shown in the figure. The charge per unit length is λ. We assume λ > 0. The point P lies on the x-axis at a distance r from the line segment.

Figure 3: A charged line segment (left) and an L-shaped junction (right).
(a) [4 points] (i) What is the total charge of the segment? (ii) In what direction does the field at P point? Explain briefly (one or two sentences).
(b) [4 points] Consider the infinitesimal segment of length dy shown in the figure. What is the electric field at P due to this infinitesimal segment? Give your answer in terms of ϵ0 ,λ,dy,y, rand the unit vectors i(ˆ) and j(ˆ). Here y denotes they co-ordinate of the infinitesimal segment.
(c) [4 points] Integrate your result of part (b) to obtain the total electric field at P due to the whole line segment. Give your answer in terms of ϵ0 ,λ,ℓ,r and the unit vectors i(ˆ) andj(ˆ).
Useful integrals.
 (3)
(3)
(d) [4 points] What form do you expect the electric field to have very far from the segment? Simplify your result of part (c) for r > ℓ .
(e) [4 points] A second identical segment is now placed parallel to the x-axis so that the two segments together form an L-shape as shown in the figure. A is a point that lies at a distance ℓ from both segments. Using your result of part (b) write an expression for the electric field at the point A. Give your answer in terms of ϵ0 ,λ,ℓ,r and the unit vectors i(ˆ) and j(ˆ).
4. A split ring.

Figure 4: (Left panel) A semi-circular ring with positive charge. (Right panel) Two semi- circular rings. The upper ring (dashed line) is positively charged; the lower ring (solid line) is negatively charged.
(a) [10 points] A semi-circular ring of radius a is uniformly charged with charge per unit length λ. Assume λ > 0.
(i) In what direction does the electric field point at the center of the ring? Be specific about the direction. For example if it is vertical, is it up or down? If horizontal, left or right?
(ii) Consider an infinitesimal segment that subtends an angle dθ and is located at an angle θ relative to the x-axis. What is the electric field at the origin due to this infinitesimal
segment? Give your answer in terms of ϵ0 ,λ,dθ,a,θ, i(ˆ) andj(ˆ).
(iii) Integrate your result of part (ii) to obtain the total electric field at the center of the circle. Helpful integrals: 'dθ sinθ = −cosθ and'dθ cosθ = sinθ .
(b) [10 points] Now suppose that a second semi-circular ring is placed below the first one as shown in the figure. Suppose that the second ring has a negative charge with charge density −λ .
(i) What is the direction of the electric field at the origin due to the second ring?
(ii) Write an expression for the electric field at the origin due to the entire second ring. Give your answer in terms of ϵ0 ,λ,a, i(ˆ) andj(ˆ). [Hint: No integration is needed. You may borrow
freely from your results of part (a)].
(iii) What is the total electric field at the origin due to both rings?
5. Uniformly charged cylinder. An infinite cylinder with radius R is uniformly charged with a charge density ρ. We assume ρ > 0. Note that the cylinder is not hollow, it is filled with charge.
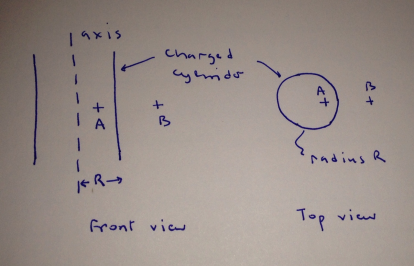
Figure 5: Front and top views of an infinite uniformly charged cylinder.
(a) [5 points] What is the direction of the electric field at the points marked A and B in fig 5? Explain your answer briefly.

Figure 6: Uniformly charged cylinder with a co-axial cylindrical Gaussian surface.
(b) [15 points] The Gaussian surface in fig 6 is a cylinder of height ℓ and radius r, with r < R. The axes of the Gaussian surface and charged cylinders coincide.
(i) What is the flux through the Gaussian surface? Give your answer in terms of E,r, R and ℓ . Here E denotes the magnitude of the electric field at a distance r from the axis of the charged cylinder.
(ii) What is the charge enclosed by the Gaussian surface? Give your answer in terms of ρ,r, R and ℓ .
(iii) Use Gauss’s law to determine the magnitude of the electric field E. Give your answer in terms of ρ,R, r and ϵ0 .

Figure 7
6. Cylindrical shell. Consider a cylindrical shell of inner radius a and outer radius b with length L and a uniform charge density ρ . For simplicity we will assume that L → ∞ . We wish to determine the electric field at the points marked A, B and C which are located at a distance r1 , r2 andr3 respectively from the axis of the cylinder. Obviously r1 < a, a < r2 < b and r3 > b.
(a) (i) In what direction does the electric field point at C? You may assume ρ > 0.
(ii) Draw a Gaussian surface suitable for determining the electric field at C.
(iii) What is the charge enclosed by the Gaussian surface?
(iv) What is the flux through the Gaussian surface?
(v) What is the electric field at C?
(b) Repeat problem (a) for the point B.
(c) Repeat problem (a) for the point A.
2023-07-19