Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Stat GR5701 Sample Final Questions

Please answer the following questions as best as you are able. The final is due at the end of the exam period unless you have prior arrangements. It is closed-book and closed-notes. Simplify any calculations as much as you are able - symbolic answers will receive full credit. You may tear off the cheat-sheet pages at the end.

As always show your work for full credit.

1) A cab was involved in a hit and run accident at night on a dark street corner in lower Manhattan. In general, 85% of the cabs in the area are yellow and 15% are green (green cabs in NYC are for the outer boroughs and upper Manhattan - they can drop off but not pick up fares downtown). The court tested the reliability of an eye witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified the color of yellow cabs 80% of the time and correctly identified green cabs 90% of the time.

a) If a random cab is sampled, what is the probability that the eye witness can correctly identify it?

b) If the eye witness identified the cab involved as being green, what is the probability that the cab involved in the accident actually was green rather than yellow?

5) The Weibull distribution can be used to model “time-to-failure” in which the failure rate is proportional to a power of time survived. A random variable has a Weibull distribution with parameters λ and k if its probability density function is:

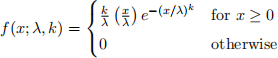
Suppose that you have a random sample of size n from a Weibull distribution distribution, X1, . . . , Xn, and that k is known.

a) (2pts) Write down the likelihood function of λ.

b) (3pts) Find the maximum likelihood estimator of λ.

10) If we conduct a single, one-sided hypothesis test, we can write down the p-value associated with it as p = P {T > tobs}, where T is a test statistic and tobs is the observed value of that test statistic for a single set of data. Suppose that instead of conducting a single hypothesis test, we collect many independent data sets, repeat the test by computing a p-value in each one, and analyze the distribution of those p-values. In this context, the p-value is a random variable and we can write it as function of the samples of observed data, i.e. PV = P {T > tobs | Tobs = tobs}.

a) (2pts) If the null hypothesis is true, show that the distribution of a random p-value, PV , has a uniform distribution on [0, 1] by calculating its cumulative distribution function. You can assume that the CDF of the test statistic T, denoted as FT (t) admits an inverse everywhere, (p).

b) (3pts) If 200 p-values are collected under the same experimental conditions and 4 are highly significant (less than 0.01), 13 are significant (between 0.01 and 0.05) and the remainder are above 0.05, conduct a goodness-of fit test that the null hypothesis is true and the p-values come from a uniform distribution.