Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

OPTIMISATION

1. a) Suppose one has three optimization algorithms which generate sequences {xa,k}, {xb,k}, and {xc,k}, as follows:

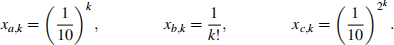
Show that all sequences converge to x ? = 0, and that the sequence {xa,k} converges linearly, the sequence {xb,k} converges superlinearly, and the sequence {xc,k} converges quadratically. [ 6 marks ]

b) Let α be a positive constant. Consider the function f(x) = αx − lnx, defined for x > 0, and the problem of minimising f using Newton’s method.

i) Determine the global minimiser of f . [ 2 marks ]

ii) Show that the function f is convex. [ 2 marks ]

iii) Write Newton’s iteration for the minimization of f and show that the resulting iteration converges to the global minimizer of f with quadratic speed of convergence. [ 6 marks ]

c) It is a well-known fact that Newton’s method is invariant to linear transformations, that is transformations of the form y = Ax, with A square and invertible. To see this, consider the functions f(x) and f(A −1 y) and let {xk} and {yk} be the sequences generated by Newton’s iteration for the minimisation of f(x) and of f(A −1 y), respectively. By writing Newton’s iterations for the two sequences show that the condition y0 = Ax0 implies yk = Axk for all k > 0. [ 4 marks ]

2. Consider the so-called water-filling problem of dimension two, that is the optimization problem

min −ln(2+x1)−ln(3+ε +x2),

x1, x2

x1 +x2 −1 = 0,

x1 ≥ 0,

x2 ≥ 0,

where ε is a small positive constant.

a) Using constraints elimination applied to the equality constraint determine a solution of the considered problem. [ 2 marks ]

b) Assume ε = 0.

i) Write fifirst order necessary conditions of optimality for the considered problem. [ 2 marks ]

ii) Using the conditions in part b.i) determine a candidate optimal solution. [ 6 marks ]

iii) Using the result of part b.ii) show that the condition of strict complementarity does not hold for the candidate optimal solution. Provide an explanation for this. [ 2 marks ]

c) Assume ε ≠ 0, but small (positive and negative). Show that the candidate optimal solution for the considered problem is described by the equations

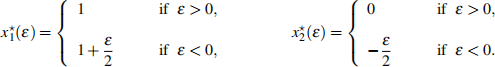
[ 8 marks ]

3. Consider the optimization problem

min −x1,

x1, x2

x2 −(1−x1) 3 ≤ 0,

−x2 ≤ 0,

a) By plotting the admissible set and the level lines of the objective function determine the optimal solution of the problem. Show that not all points are regular points for the constraints. [ 4 marks ]

b) Write fifirst order necessary conditions of optimality for the problem. [ 2 marks ]

c) Show that the necessary conditions of optimality do not provide any candidate optimal solution and explain why this is the case. [ 6 marks ]

d) Consider the so-called log-barrier function, that is the function

with ε > 0. Show that the point xε = (1−6ε,108ε 3 ) is a local minimizer of Bε for all ε > 0. Hence, argue that, as ε → 0, the point xε converges to the optimal solution of the considered problem. [ 8 marks ]