Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

EC2020

Summer Examinations 2020/21

Microeconomics 2

Section A: Answer ALL FOUR questions

1. Consider an individual, Claire, facing the following gamble. With probability ρ = 1/10 she will end up in a “bad state” and consume xb = 5 and with probability 1 − ρ = 9/10 she will consume xg = 500 in a “good state”. Consider another individual, Rik, who will end up in the same “bad state” with probability σ = 1/5 and in the same “good state” with probability 1 − σ = 4/5. Claire’s and Rik’s utility can be represented as u(xi) = xi α , where i = g, b and α ∈ (0, 1].

(a) Derive the coefficient of, respectively, absolute and relative risk aversion and comment on the two individuals’ attitudes to risk. (3 marks)

(b) Suppose an insurance company offers Rik and Claire £5 of insurance for a premium of £1. How much insurance will Rik and Claire, respectively, buy, and how much will they consume, respectively, in each state? Assume α = 1/2. (5 marks)

(c) How much profit would the insurance company make under the contracts offered in the previous subquestion? (5 marks)

(d) Suppose Claire’s utility function were state dependent. Specifically, assume her utility in the good state is u(xg ) = xg(1)/2, and her utility in the bad state is u(xb ) = x How     much insurance would Claire now purchase given that the probability of the bad state   occurring and the price of insurance remain the same?   (5 marks)

2.  Consider the following game:

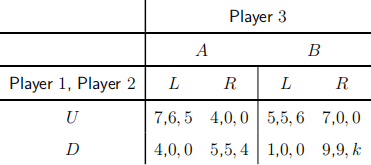
(a)  Identify all pure-strategy Nash equilibria assuming k = 1.   (3 marks)

(b)  Identify all Pareto efficient outcomes of the game for k = 1.   (3 marks)

(c) Suppose the game is played twice. Is there a subgame perfect Nash equilibrium (or equilibria) which involves an outcome in the first stage which is not a Nash equilibrium in the one-off stage game assuming players do not discount period 2 payoffs and that  k = 1?   (6 marks)

(d) Suppose again that the game is played twice. For which values of k is there a subgame perfect Nash equilibrium in which players play (D, R, B) in period 1 and (U, L, B) in   period 2?   (6 marks)

3.  Consider a 2 × 2 pure exchange economy with two consumers, Andy and Beth, or {A, B}, and two goods {1, 2}. Andy has endowment eA  = (2, 2) and Beth has endowment

eB  = (4, 2). Andy’s preferences can be represented by the utility function uA  = xA1 + xA2 and Beth’s preferences can be represented by the utility function uB  = xB1xB2 .

(a) Calculate both players’ marginal rates of substitution at the initial endowment andexplain whether the initial endowment is Pareto efficient.  (4 marks)

(b) Sketch an Edgeworth box showing the dimensions, initial endowment and both players’ indifference curves through the initial endowment.  (4 marks)

(c) Show that the allocation xA  = (2, 0), xB  = (4, 4) is Pareto efficient. Use this to find the Pareto Set. (4 marks)

(d)  Can every Pareto efficient allocation be supported as a Walrasian Equilibrium for some choice of initial endowment? Justify your answer as fully as you can.  (6 marks)

4.  Consider a Robinson Crusoe economy with two goods: leisure time and food. The consumer, Crusoe has 20 units of leisure time (good 1) and no units of food (good 2). They have         preferences given by the utility function u = x1 x2  where xi  is Crusoe’s consumption of good i ∈ {1, 2}. Crusoe is able to work to produce food: for every k ≥ 0 units of time they spend collecting food, he collects 2^k units of food.

(a)  Find the optimal amount of time Crusoe should spend collecting food and illustrate it on a diagram. (4 marks)

(b) Model this situation in the Walrasian Equilibrium framework: State the firm’s production set and discuss how Crusoe and the firm interact.  (3 marks)

(c)  Find the Walrasian Equilibrium. (8 marks)

(d) State the First Fundamental Theorem of Welfare Economics and discuss it in relation to this example. (3 marks)

Section B: Answer ONE question.

5. Consider the following three-player game:

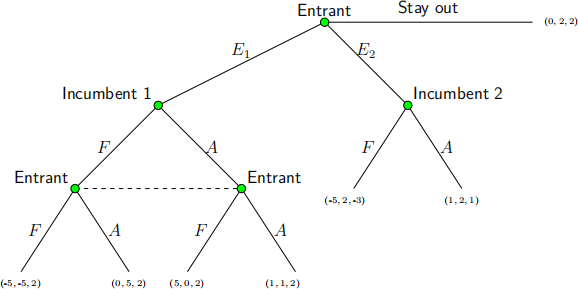
A potential entrant is considering whether to enter into market 1 (play E1), or market 2 (play E2) or to stay out of both markets. The Entrant moves first. If it enters market 1, it will play a simultaneous-move game with the incumbent firm in that market called Incumbent 1. In this subgame, the Entrant and Incumbent 1 simultaneously decide whether to play Fight (F) or Accommodate (A). Alternatively, the Entrant can enter into market 2 (or play E2) where the incumbent in that market (Incumbent 2) has a first-mover advantage. Incumbent 2 can play either Fight (F) or Accommodate (A). The Entrant also has the option to stay out of either market. The payoffs in the game are denoted (x, y, z), where the first entry is the payoff to the entrant, the second is the payoff to Incumbent 1, and the third is the payoff to Incumbent 2.

(a) How many subgames are there in this game? (2 marks)

(b) Represent this game in normal form (table form). (4 marks)

(c) Identify all pure-strategy Nash equilibria of the game. (8 marks)

(d) Which of the pure-strategy Nash equilibria that you identified in the previous subquestion are subgame perfect? (8 marks)

(e)  Suppose the game is played twice and that neither player discounts period 2 payoffs.  Is there a subgame perfect Nash equilibrium in which in the first period, the Entrant enters market 1 with the Entrant playing A and Incumbent 1 playing F , followed by a second period in which Entrant enters market 1 but with Entrant playing F and Incumbent 1 playing A?  In both periods, Incumbent 2 plays A.   (6 marks)

6. On a warm day in May, a group of five Warwick students (in order of age A, B, C, D and E with A the oldest) decide to go for a walk on campus to take a break from revising for their EC202 exam. They enter a fairly secluded part of campus and by accident, they discover a hidden box containing £1000. They must now decide how to distribute it between them and they agree on the following rules. The oldest student first proposes a plan of distribution. The students, including the proposer, then vote on whether to accept the proposal. If the majority accepts the plan, each student receives their share according to the proposal and the game ends. If there is a tie, the proposer has the casting vote. If the majority rejects the plan, the proposer is ostracised (sent to Coventry!), and the second oldest student makes a new proposal to begin the system again. The process is repeated until a plan is accepted or only one student (the youngest) is left.

Payoffs are as follows. First, each Warwick student does not want to be ostracised and would receive a payoff equal to -100 (in monetary terms) if this happens. Second, given they’re not ostracised, they want to maximise their share of the find. Third, each student prefers to ostracise another (each player receives a small payoff equal to 1 for ostracising one of the other students) if all other results would otherwise be equal. Find an allocation which can be supported as a subgame perfect Nash equilibrium in this game. (Hint: use backwards induction). (28 marks)

7. Consider a 2 × 2 pure exchange economy with two consumers, Andy and Beth, or {A, B}, and two goods {1, 2}. Andy has endowment e A = (1, 3) and Beth has endowment e B = (3, 1). Andy’s preferences can be represented by the utility function uA = xA 1 xA2 and Beth’s preferences can be represented by the utility function uB = xB1xB2 that Andy’s consumption of good 1 creates a negative externality for Beth. − 2xA1. Notice

(a) Find the Walrasian Equilibrium. (5 marks)

(b) Justify that in economies without externalities, each player does at least as well in Walrasian Equilibrium than from their initial endowment. (3 marks)

(c) Compute Beth’s utility at the initial endowment and at the Walrasian Equilibrium. (2 marks) 

(d)  Explain why Beth has a lower utility at the Walrasian Equilibrium than at the inital endowment. (2 marks)

(e)  Show that the Walrasian Equilibrium is not Pareto efficient by finding an alternative allocation that Pareto dominates it .  Explain your steps in finding such an allocation . (5 marks)

(f) Suggest measures a benevolent social planner could take to intervene in this market to make it efficient and discuss any issues with its implementation.  (5 marks)

(g) To deal with issues like negative externalities, societies require a form of government,    typically elected by the people. Using your social choice theory knowledge, discuss the   difficulty of choosing an alternative in a way that fairly reflects the views of the society’s inhabitants. (6 marks)

(i) Argue that every core allocation gives all null players a payoff of 0. (4 marks)