EC2020 Microeconomics 2 Summer Examinations 2019/20
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
EC2020
Summer Examinations 2019/20
Microeconomics 2
Section A: Answer ALL FOUR questions
1. Consider an individual, Becky, facing the following gamble. With probability ρ = 1/5 she will end up in a “bad state” and consume xb = 0, and with probability 1 − ρ = 4/5 she will consume xg = 1000 in a “good state”. Consider another individual, Gareth, who will end up in the same “bad state” with probability σ = 2/5 and in the same “good state” with probability 1 − σ = 3/5. Becky’s and Gareth’s utility can be represented as u(xi) = xi α , where i = b, g and α < 1.
(a) How much insurance will Becky and Gareth, respectively, buy if they are each offffered an actuarially fair insurance? And how much will they consume in each state? (5 marks)
(b) Assume α = 1/2. Is there a self-selecting separating equilibrium in which Gareth buys full insurance whereas Becky buys less than full insurance? And if so, how much insurance will Becky buy? Illustrate the equilibrium in a diagram clearly indicating the amounts of consumption of, respectively, Becky and Gareth, in the good and bad state with their respective insurance contracts. (8 marks)
(c) Suppose Becky’s utility function were state dependent. Specifically, assume her utility in the good state is u(xg ) = xg(1)/2, and her utility in the bad state is u(xb ) = x![]() If we assume that Gareth’s preferences were as above, would it be possible to offer Becky an actuarially fair insurance which Gareth would not choose over his own full insurance contract? (5 marks)
If we assume that Gareth’s preferences were as above, would it be possible to offer Becky an actuarially fair insurance which Gareth would not choose over his own full insurance contract? (5 marks)
2. Consider the following game:

(a) Identify all pure-strategy Nash equilibria assuming k = 2. (6 marks)
(b) Is there a mixed-strategy Nash equilibrium assuming k = 2? (6 marks)
(c) Suppose the game is played twice. For which values of k is there a subgame perfect Nash equilibrium, which involves an outcome in the first stage that is not a Nash equilibrium in the one-off stage game, assuming players do not discount period 2 payoffs? (6 marks)
3. Consider a 2 × 2 pure exchange economy with two consumers, Andy and Bob, or {A, B}, and two goods {1, 2}. Andy has endowment eA = (2, 2) and Bob has endowment eB = (4, 1). Andy’s preferences can be represented by the utility function uA = xA1xA2 and Bob’s preferences can be represented by the utility function uB = min {xB1, xB2}. Let prices be p = (1, 1)
(a) Sketch an Edgeworth box, clearly labelling their initial endowment, budget sets and indifference curves. (5 marks)
(b) Write down Bob’s utility maximisation problem as a function of prices, p = (p1 , p2 ) ∈ R![]() 0 and verify that his optimal demand is
0 and verify that his optimal demand is
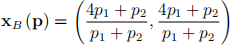
Show your working. (2 marks)
(c) Andy’s optimal bundle is
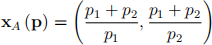
(i) Find both players’ optimal demands at prices p = (1, 1). (1 mark) (ii) State Walras’ Law and show it holds at prices p = (1, 1). (3 marks)
(d) Draw an Edgeworth box illustrating players’ optimal demands and the excess demand or supply of each good. (3 marks)
(e) On an Edgeworth box sketch:
(i) The Pareto Set and contract curve.
(ii) The Walrasian Equilibrium prices and allocation.
You do not need to give any mathematical calculations to find the Walrasian Equilibrium, but you should justify your sketch in words. (4 marks)
4. Consider the following 2 × 2 pure exchange economy with two consumers, Andy and Bob, or
{A, B}, and two goods {1, 2} . Both have an initial endowment of two units of each good . Andy’s preferences can be represented by the utility function uA = xA1xA2 − xB1 . Bob’s preferences can be represented by the utility function uB = xB1xB2
(a) Define the economic concepts of “externality” and “The First Fundamental Theorem of
Welfare Economics”. Discuss whether they apply to this example. (5 marks)
(b) Verify that there is a Walrasian Equilibrium with prices p = (1, 1). Explain intuitively
why this Walrasian Equilibrium is not Pareto efficient and give an example of an alternate allocation that Pareto dominates it. (5 marks)
(c) Their friend Sam is an amateur social planner and thinks he has a solution. He issues Andy with some number V ≥ 0 vouchers, which Andy may keep or sell to Bob. Furthermore, Sam enforces the mechanism that for Bob to consume k ≥ 0 units of good 1, he must be in possession of at least k vouchers. Will the Walrasian Equilibrium be Pareto efficient? Does it depend on the number V? (You don’t need to calculate the Walrasian Equilibrium) (3 marks)
(d) Many democracies around the world use the system of “plurality” to elect their leaders. Under this system each person gets one vote and the candidate who receives the most votes wins. Briefly discuss some advantages and/or disadvantages of this system, preferably referring to some of the technical terms discussed in Social Choice Theory.
(5 marks)
Section B: Answer ONE question.
Please use a separate booklet
5. Consider the following three-player game:
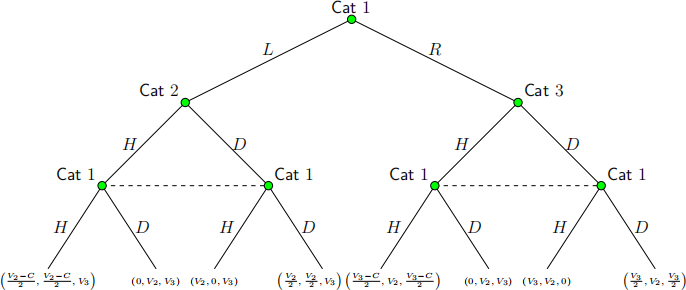
Cat 1 is very hungry and considering whether to fight Cat 2 or Cat 3 for food. Cat 2 and Cat 3, respectively, each have food. If Cat 1 opens the game by playing L, it will enter a fight with Cat 2. Each cat then simultaneously choose whether to play Hawk (H) or Dove (D).
Cat 1 can alternatively open the game by playing R in which case it will enter a simultaneous-move fight with Cat 3, where each cat can play H or D. The cost of entering a fight is the same for all cats and equal to C. Cat 1 and Cat 2 value Cat 2’s food at V2, and
Cat 1 and Cat 3 value Cat 3’s food at V3. The probability that any cat wins a fight is 12, and it is assumed that if both players play D, they will get the food with equal probability. The expected payoffs to each player is indicated in the figure above at each terminal node, where the payoff (x, y, z) implies Cat 1 gets x, Cat 2 gets y and Cat 3 gets z. For example, if Cat 1 selects L, followed by Cat 1 and Cat 2 both playing H, Cat 1 and Cat 2 both receive expected payoffs (V2−C 2) and Cat 3 receives V3.
(a) Suppose the cost of a fight is C = 10, and the value of respectively, Cat 2’s and Cat 3’s food, are V2 = 5 and V3 = 20. Identify all subgame-perfect Nash equilibria, and the payoffs to each player in each subgame-perfect Nash equilibrium. (8 marks)
(b) The cost of a fight is still C = 10 as in the previous subquestion, and the value of Cat 2’s food remains at V2 = 5 . Suppose, however, that the value of Cat 3’s food is now V3 = 12 . What are the subgame-perfect Nash equilibria in this case, and what are payoffs in each subgame-perfect Nash equilibrium? (8 marks)
(c) Suppose Cat 1 and Cat 2 play the following game:
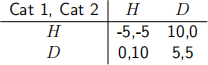
Suppose also that they agree to observe the following mechamism: a random device selects one cell in the game matrix with the probabilities give in Table 1 . The probabilities given in the table are common knowledge. When a cell is randomly selected an ‘umpire’ tells each player what to play. Show that this mechanism can be supported in a correlated equilibrium. If so, what would be the payoffs to Cat 1 and Cat2? (6 marks)
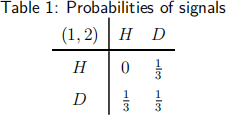
(d) Suppose in the previous subquestion, Cat 1 and Cat 2 simply played strategies according to the mixed-strategy Nash equilibrium. Would their payoffs in the mixed-strategy Nash equilibrium exceed those in the correlated equilibrium? (6 marks)
6. Consider the following version of the Traveler’s dilemma, which was initially proposed by economist Kaushik Basu. An airline loses two suitcases belonging to two different travelers, which we label Traveler 1 and Traveler 2. The two suitcases are identical and contain identical antiques. The airline manager assigned to settling the travelers’ claims informs them that the airline is liable for a maximum of £100 per suitcase. The airline is unable to ascertain the true value of the antiques. To determine an honest appraised value of the antiques, the manager separates the travelers such that they are unable to communicate. At the same time, the travelers are asked to write down the value of the antiques at no less than £20 and no larger than £100. The travelers are informed that if they write down the same number, this will be treated as the true value of the antiques and they will be reimbursed that
amount . However, if one traveler writes down a smaller number than the other, the smaller
number will be taken as the true value, and both travelers will receive that amount along with a reward/penalty. An additional £21 will be paid to the traveler reporting the smaller
number, and a deduction equal to £20 will be taken from the traveler reporting the higher amount. For simplicity, we restrict the amounts the travelers are permitted to report to multiples of 20. Formally, the set of actions avaiable to the players are:
S1 = S2 = {20, 40, 60, 80, 100}.
(a) Write down this game in a table in normal form. (6 marks)
(b) What is (are) the Nash equilibrium (equilibria) of this game? (6 marks)
(c) Suppose this game is played T times. How many subgames are there in this repeated game? (10 marks)
(d) What is (are) the subgame-perfect Nash equilibrium (equilibria) of the repeated game? (6 marks)
7. Consider a Robinson Crusoe economy with two goods: leisure time and food. The consumer, Crusoe has 12 units of leisure time (good 1) and no units of food good 2. He has preferences given by the utility function u = x1 + x2 . Crusoe is able to work to produce food: for every k ≥ 0 units of time he spends collecting food, he collects 4^k units of food.
(a) Find the optimal amount of time Crusoe should spend collecting food and illustrate it on a diagram. (4 marks)
(b) Model this situation in the Walrasian Equilibrium framework: State the firm’s production set and discuss how Crusoe and the firm interact. (3 marks)
(c) Find the Walrasian Equilibrium and illustrate it on a diagram. (11 marks)
Consider the following three player cooperative game of transferable utility:
|
S |
∅ |
{1} |
{2} |
{3} |
{1, 2} |
{1, 3} |
{2, 3} |
{1, 2, 3} |
|
v (S) |
0 |
4 |
0 |
1 |
4 |
5 |
7 |
12 |
(d) Explain what super-additivity means and whether this game satisfies it. (3 marks) (e) Find the Shapley value of this game. (7 marks)
8. Two housemates Andy and Bob or {A, B} are deciding how much money to spend on Christmas decorations for their house and how much to keep for themselves.
(a) Explain what a public good is and discuss the extent to which Christmas decorations can be seen as a public good. (3 marks)
(b) In Nash Equilibrium, would you expect the total amount of Christmas decorations to be
more or less than the optimal amount? Explain why. (3 marks)
For i ∈ {A, B}, let xi ∈ [0, 4] be the amount person i spends on Christmas decorations. Let Andy ’s utility be uA = 2^xA + xB − xA and Bob’s utility be uB = 2^xA + xB − xB .
(c) Find the Nash Equilibria. Which of these Nash Equilibria is symmetric? (5 marks)
(d) Find the socially efficient level of Christmas decoration and verify that utility can be transferred from one player to another in a one to one ratio. (5 marks)
(e) Explain what a bargaining situation is and how this situation fits into that framework. (3 marks)
(f) Draw the utility possibility set and show the disagreement point, which we model as the symmetric Nash Equilibrium. (3 marks)
(g) Find the Nash Bargaining solution of this game and illustrate it on your diagram. How much Christmas decorations does each player provide? (3 marks)
(h) Instead suppose players negotiate by the ultimatum game: Andy issues Bob with a “take it or leave it offer”, where the Nash Equilibrium occurs if the offer is rejected . What is the solution of this game? (3 marks)
2023-06-30