CO 250 Spring 2023: Assignment 5 problems
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CO 250 Spring 2023: Assignment 5 problems
Due: Tuesday June 20 at 4:30pm EST
A5-1. Canonical Forms
(a) Consider the following LP in standard equality form.
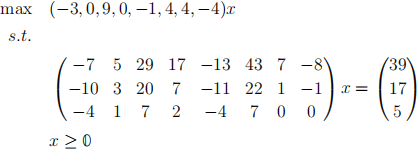
For each of the following vectors, determine whether or not it is a basic feasible solution to the given LP. Justify your answers.
If the vector is a basic feasible solution, find a corresponding basis, and derive an equivalent LP in canonical form for your basis. Show all the work in deriving the canonical form.
(i) (2, 0, 3, 0, 2, 0, 0, 1)T
(ii) (0, 5, −1, 0, 0, 1, 0, 0)T
(iii) (1, 0, 1, 1, 0, 0, 0, 0)T
(iv) (0, 0, 0,52, 0, 0,12, 1)T
(v) (0, 1, 0, 2, 0, 0, 0, 0)T
(vi) (0, 9, 0, 0, 1, 0, 1, 0)T
(b) Consider two LPs
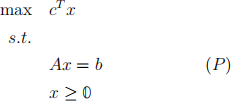
and
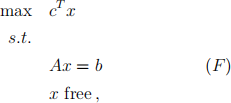
where A has linearly independent rows.
(i) Prove that if (F) has an optimal solution, then c = AT z for some vector z.
(ii) Prove that if (F) has an optimal solution, then in every canonical form of (P), the objective function is 0 T x + q, where q is a constant.
A5-2. Simplex Method
Perform the simplex algorithm on the following LPs, starting with the given basis. Use Bland’s Rule when you have multiple choices of entering or leaving variables. You may use the method of canonical forms, dictionaries, or the tableau method. In an iteration, you should show how you are determining the entering and leaving variables, and state the new basis and basic feasible solution. You may then directly record the canonical form, dictionary, or tableau associated with the new basis without showing work.
If the problem has an optimal solution, give a certificate of the optimality of your optimal solution. If the problem is unbounded, give the certificate of unboundedness, and give a feasible solution whose objective value is at least 2023.
For this problem, keep non-integer values as exact fractions.
Note: You are allowed to use computational tools to calculate the canonical forms / tableaus.
(a) B = {5, 6}
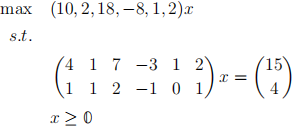
(b) B = {1, 3, 5, 6}
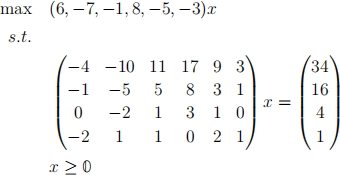
A5-3. Changes in the Input Data
Given an LP
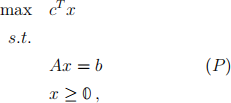
where A has linearly independent rows, a basis B of A is called optimal if B is feasible and in the canonical form corresponding to the basis B all coefficients in the objective function are nonpositive. Using the proposition about canonical forms from the lectures, we can rewrite this definition as follows: B is an optimal basis if A −1Bb ≥ 0 and c − AT y¯ ≤ 0, where y¯ = A−TBcB.
(a) Consider the following linear program (LPθ) defined for a scalar θ ∈ R. Here, θ is not a variable but a parameter: an unknown but fixed number.
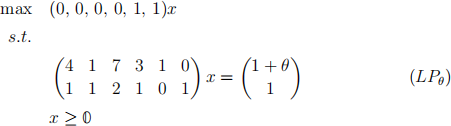
Prove that the basis B := {5, 6} is an optimal basis for (LP0). Determine all values θ for which B is an optimal basis for (LPθ).
(b) Given a matrix A, vectors b, b ′ and c, consider the linear program (Pθ) defined by a scalar θ ∈ R. Here, θ is not a variable but a parameter: an unknown but fixed number.
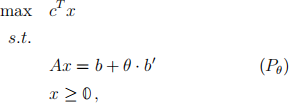
Let us assume that the basis B is an optimal basis for the linear program (P), i.e. is an optimal basis for the linear program (P0). Determine the range of θ for which B is an optimal basis for (Pθ). The range should depend only on the given matrix A, basis B and vectors b, c, b ′ .
(c) Let us consider θ ∈ R, such that the basis B is an optimal basis for both the linear program (P0) and for the linear program (Pθ) from part (b). Let Val0 denote the optimal value of (P0), and Valθ denote the optimal value of (Pθ). Write a formula for Valθ−Val0. The formula should depend only on the given matrix A, basis B and vectors b, c, b ′ , θ.
2023-06-21