The formulas below may be used without proving them.

1.  Laplace transforms

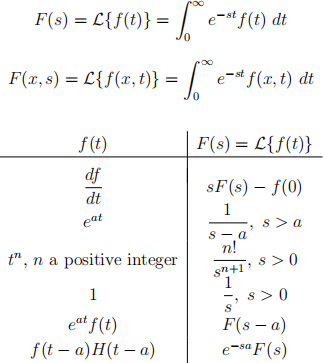
2.  Fourier transforms

1.  (14 marks)

(a)  Let f (x) be the piecewise function defined as

f (x) = 1   1--xx<<10,

Define F (x) as the periodic extension of f (x). The function F (x) has period two. The Fourier Series for F (x) can be written as

 bn cos 

Find bn , n = 1, 2, . . ..

(b) Define EN (x) as the error

EN (x) =  bn cos  < F (x)

Sketch the graph of Eì↓  for x ∈ [<1.5, 1.5] by hand.  Do not use a computer program to find the graph.

(c) How would the graph E4↓  differ from the graph of Eì↓ ?  Justify your answer.

2.  (18 marks) Let u(x, t) denote the solution to the pde

ut  = uxx  + u,    0 < x < 1, t > 0,

with the boundary conditions u(0, t) = 0, u(1, t) = 1, and the initial conditions u(x, 0) = sin(πx/2).

(a) Find the steady-state solution us (t).

(b) Let U (x, t) = u(x, t) < us (x). Find the partial differential equation for U.  Then find the boundary conditions and initial conditions for U.

(c)  Use the Separation of Variables technique to find the general solution for U that satisfies the boundary conditions for U.

(d)  Suppose the initial conditions u(x, 0) = sin(πx/2) were changed to u(x, 0) = x(1 < x). How would the general solution from the previous part of the question change? Justify your answer.

3.  (8 marks) Consider the problem

uxx + ugg  = 0,       0 < x,y, < 2,

u(0, y) = 0   u(2, y) = 1,

u(x, 0) = 0,    u(x, 2) = 0.

(a) The eigenfunctions for this problem can be written as the product of a sinh function and a sin function.  Will the sin function be of the form sin αnx or sin βny where αn and βn  are suitably chosen constants?  Use the boundary conditions for the problem to justify your answer. Do not find the general solution to the problem.

(b) The boundary condition u(2, y)  =  1  gives u(2, 2)  =  1,  and  the boundary  condition u(x, 2) = 0 gives u(2, 2) = 0.  Hence the boundary conditionsimply u has a discontinuity at (2, 2). Can the Separation of Variables technique be used to solve the above problem? Justify your answer.

4.  (20 marks) Consider the diffusion equation

ut  = uxx ,    0 < x < o ,    0 < t < o

with the boundary conditions

u(x, 0) = f (x)

ux (0, t) = 0

u o 0 as x, t o o

(a) Explain why it is difficult to solve this problem using Laplace transforms methods.

(b)  Solve this equation using Fourier transforms.  You may have to extend the domain to achieve this. Your final answer will be a convolution.

ut + 2ux  = 0,    u(x, 0) = <1,    u(0, t) = 1

Your friend claims that a weak solution to this equation is:  u(x, t)  =  1 when t > x and u(x, t) = <1 if t - x.

(a) What does your friend mean when they claim u is a weak solution?  Write out their claim as an integral equation using the definition of weak solutions.  Because u(x, t) is defined piecewise, it may be useful to break your integral up into two separate integrals.

(b) Evaluate your integral equation in order to demonstrate that u(x, t) is not a valid weak solution for the equation given.