The formulas below may be used without proving them.

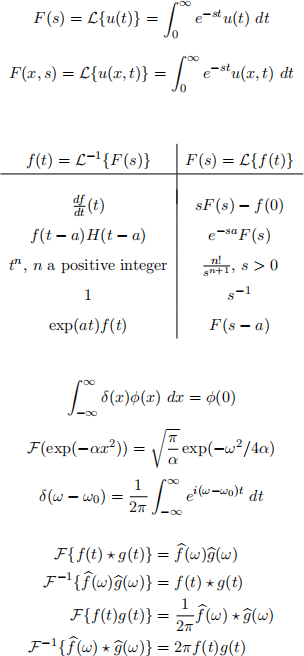
1.   (a)  (Total marks  18) The Fourier series of a function f (t) defined on the interval  [-π, π] can be written as

a2 + a ncos(nx) + bn sin(nx)

where

a2 = mm f (x) dx,    an  = mm f (x) cos(nx) dx,    bn  = mm f (x) sin(nx) dx

Let δ(x) denote the dirac delta function. Find the Fourier series of δ(x) in the distributional sense.                                                                                                                               (6 marks)

(b) Let H be defined as

H(x) = { 1(0)   0(x)  x(0),

Use the definition

< f} , φ >= - < f, φ}  >

to find the distributional derivative of H(-t).                                                        (6 marks)

(c)  Show that

δ(x2 - a2 ) =  [δ(x + a) + δ(x - a)]

[Hint: Use the substitutions x = ′u and x = -′u .]                                                     (6 marks)

2.  (Total marks 16) This question is about finding the solution u(x, t) to the following problem using Laplace Transforms.

ut = c2uzz ,    0 < x < o , t > 0,

u(x, 0) = T2 ,    0 < x < o ,

u(0, t) = 0,    0 < t < o ,

u(x, t) → 0,    as   x → o .

(a) Let F (x, s) be defined as

F (x, s) = c{u(x, t)} = l2 & e –stu(x, t) dt

Use Laplace Transforms to write down a differential equation for F (x, s).                (6 marks) (b) Hence find the solution u(x, t) that satisfies the initial and boundary conditions given above.

You may assume the result that

c– 1  = 1 - erf )

where erf is the error function.                                                                                    (10 marks)

3.  (Total marks 14) The Fourier transform r(f) of the function f (x) is defined as

r{f } = l&& f (x)e –iuz  dx

Use Fourier Transforms to find the general solution to the transport equation

 + c = 0,    -o < x < o ,    t > 0,    u(x, 0) = g(x).

You may use the result that the Fourier transform of g(x - a) is exp(-iaω)G(ω) where G(ω) is the Fourier transform of g(x).

4.  (Total marks 18) Consider the boundary value problem

dx(d2) = x2 ,    u(0) = 1,    u(1) = 2.

(a) Let G(x, s) be the Green’s function for this problem. Write down

(i) the differential equation satisfied by G(x, s),

(ii) the boundary conditions satisfied by G(x, s), and

(iii) the continuity condition G(x, s) must satisfy. (6 marks)

(b) Find G(x, s).                                                                                                                   (8 marks)

(c) Use G(x, s) to calculate u(x).                                                                                      (4 marks)