The formulas below may be used without proving them.

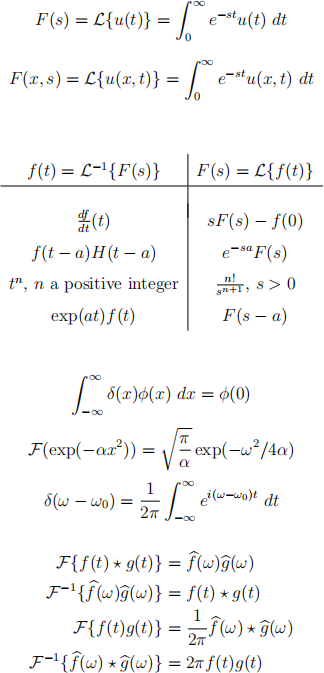
1.  (Total marks 15)

(a)  Consider first the following partial differential equation problem:

u(0, t) = 0,    u(1, t) = 0,                      t > 0,                                   (1)

u(x, 0) = f (x).

Find explicitly the steady state solution, us (x) to the problem, where us (x) satisfies the steady state equation:

us(一一)(x) + x = 0

with the boundary condition us (0) = us (1) = 0.                                               (4 marks)

(b) Define w(x, t) = u(x, t) - us (x), where us (x) is the steady state solution you found in part (a).  Write down the partial differential equation, boundary condition and initial condition satisfied by w(x, t).                (5 marks)

(c)  Consider then the following partial differential equation problem:

vt  = v乡乡,                                                0 < x < 1, t > 0,

v(0, t) = 0,    v(1, t) = -t,                      t > 0,

v(x, 0) = 0.

Explain how to define a function vs (x, t) so that w(x, t) = v(x, t) -vs (x, t) can be solved by using the solution of partial differential equation problem (1).  You should find a formula for vs (x, t) as part of your answer, but do not calculate v(x, t).          (6 marks)

2.  (Total marks 5) The Laplace transform of y(t) is defined by

c{y(t)} = Y (s) = lo ′ y(t)e′st dt.

(a) Find the Laplace transform of the function y(t) = 1.                                        (2 marks)

(b) Using the formula 

c{y一 (t)} = sY (s) - y(0),

or otherwise, derive a formula for

c {lot y(u)du} .                                   (3 marks)

3.  (a)  (Total marks 6) Let the distribution f be defined by

< f, φ >= l′′(′) f (x)φ(x) dx,

where φ(x) is a test function.

Let Ha  be defined as

Ha (x) = { 1(0)   a(x)  x(a),

Use the definition

< f\ , φ >= - < f, φ\  >

to find the distributional derivative of Ha.                                                       (2 marks)

(b) Use the definition of the delta function δ to show that

δ(ax) = δ(x),       a  0. (4 marks)

4.  (Total marks 12) This question is about finding the solution u(x, t) to the following problem using Laplace Transforms.

u乡 + xut  = 0,    0 < x < s, t > 0,

u(x, 0) = 0,    0 < x < s ,

u(0, t) = t,    0 < t < s.

(a) Let F (x, s) be defined as

F (x, s) = c{u(x, t)} = lo ′ e′stu(x, t) dt

Use Laplace Transforms to write down a differential equation for F (x, s).      (4 marks)

(b) Hence find the solution u(x, t) that satisfies the initial and boundary conditions given above.                          (8 marks)