The formulas below may be used without proving them.

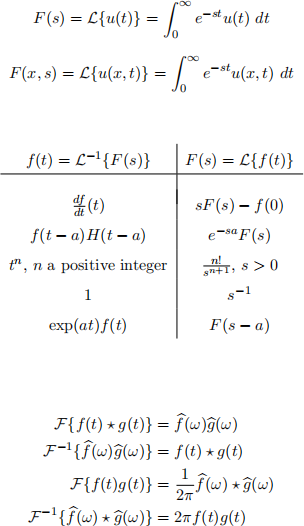
1.  (Total marks 12) Suppose f (x) = x2  when x ∈ [0, 1].

(a)  Sketch the periodic odd extension of this function on the interval  [ -3, 3]. You do NOT need to indicate what happens at any discontinuities.                                                         (4 marks)

(b)  Sketch the periodic even extension of this function on the interval [ -3, 3]. You do NOT need to indicate what happens at any discontinuities.                                                         (4 marks)

(c)  The following graph shows f (x) along with a partial sum of the sine series for f (x).

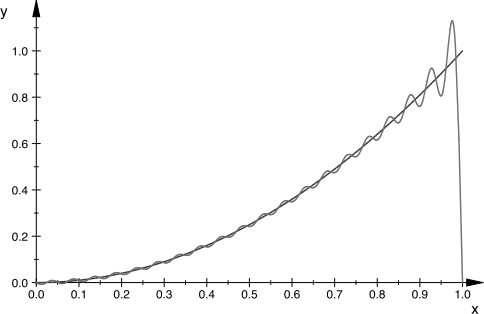
Explain why the partial sum of the sine series has large oscillations around f (x) near the endpoint at x = 1, but not near x = 0.                        (2 marks)

(d) Would you expect similar large oscillations around f (x) in partial sums of the cosine series of f (x)?  If so, where would they occur?  Why would you expect, or not expect, to see this behaviour?                    (2 marks)

2.  (Total marks 20) The following equations model heat transfer in a perfectly insulated ring of metal:

(a) Ignore the initial condition for now, and suppose that u(x, t) = X(x)T (t).  Show that, in that case, X(x) satisfies the following boundary value problem whenever u(x, t) is not identically zero:

X// (x) - βX(x) = 0

X(-π) = X(π)

X/ (-π) = X/ (π)

(6 marks) (b) What is the corresponding differential equation for T (t)?                                          (2 marks)

(c) You may  assume  (and  do  not  need  to  show) that  a  complete  linearly independent set of solutions to the boundary value problem for X(x) is given by

{1, cos(nx), sin(nx)},    n = 1, 2, . . . .

(i) Find the values of β that correspond to each function in this set.                    (4 marks)

(ii) For each element of this set, find the corresponding solution for T (t).              (4 marks)

(d) Using your answer to part (c), give the general solution to the PDE with the boundary con- ditions given above. You do not need to give a formula for the coefficients.              (4 marks)

3.  (Total marks 8) Let the distribution f be defined by

< f, φ >= loo f (t)φ(t) dt

where φ(t) is a test function.

Let H be defined as

H(x) = { 1(0)   0(x)  x(0)

Use the definition

< f/ , φ >= - < f, φ/  >

to find the distributional derivative of H(x).                                                                        (8 marks)

4.  (Total marks 16) This question is about finding the solution u(x, t) to the following problem.

ux = 2ut + u,    0 < x < &,  t > 0,

u(x, 0) = 6e-3x ,    0 < x < & ,

u(x, t) → 0   as   x → &

(a) Let F (x, s) be defined as

F (x, s) = /{u(x, t)} = l0 o e-stu(x, t) dt

Use Laplace Transforms to write down a differential equation for F (x, s).                (4 marks) (b) Hence  find  the  solution  u(x, t)  that  satisfies  the  initial  and  boundary  conditions  given above.                         (12 marks)

5.  (Total marks 10) The Fourier transform 于(ω) of the function f (t) is defined as

于{ω} = loo f (t)e-iωt  dt

Use direct integration to find the Fourier transform of

H(t - 4)e-t/4

(10 marks)

6.  (Total marks 18) The convolution w(t) of the functions u(t) and v(t) is defined as

w(t) = loo u(τ )v(t - τ ) dτ

Use the appropriate convolution theorem to find the inverse Fourier transform of

1

(1 + iω)(2 + iω)

Express your answer using the Heaviside function H(t). You may use the result that if a > 0 the

Fourier transform of

f (t) = { 0(e) -at

is

1

a + iω

t > 0

t < 0

(18 marks)