STATS 320 – Applied stochastic modelling – 2020 semester 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
STATS 320 – Applied stochastic modelling – 2020 semester 1
Final assessment
1. Consider a household with three people in it, named Alpha, Beta, and Delta. Delta has just fallen ill with a respiratory infection, so the whole household is asked to self-isolate together until no-one is ill any longer. Let Xn be the number of ill people in the household at the beginning of the nth day, with the process starting on day 0, with just Delta being
ill. On any day, each person is either ill or healthy. If someone recovers from the illness, they are healthy, but also susceptible to it again, and could catch it again (there is no immunity). We say that the disease is eliminated in the household as soon as all three members of the household are healthy (that is, no-one is ill with this disease any longer).
Suppose (Xn , n > 0} is modelled as a Markov chain with state space S = (0, 1, 2, 3} and transition probabilities given by
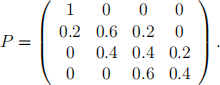
(a) (2 marks) Draw the transition diagram for this chain.
(b) (2 marks) What is the probability that Delta recovers from the illness without infecting anyone else in the household?
(c) (4 marks) What is the probability that at some time before the disease is eliminated, everyone in the household is ill at the same time?
(d) (4 marks) Let W be the maximum number of people in the household who are ill at any one time, prior to the disease being eliminated. Find the distribution of W , and hence calculate E(W). (Hint: (b) and (c) should be helpful here.)
(e) (4 marks) What is the expected time until the disease is eliminated (counting the initial day when Delta becomes ill as day 0)?
(f) (4 marks) This model makes several modelling assumptions. Pick two of those as- sumptions, and comment briefly on whether they are likely to hold or not in a realistic setting.
2. Phone calls arrive at my phone as a Poisson process with rate λ = 8 per hour. The times I spend talking to each caller on the phone have a lognormal distribution with mean 5 minutes and standard deviation 4 minutes, independently of other calls and of the call arrival process. Calls which come in while I am already talking on the phone are placed on hold, in a first-come-first-served queue. There is no limit to the number of callers who may be on hold at any one time.
(a) (1 mark) Describe this queueing system in A/S/m/n notation.
(b) (3 marks) Find the steady-state average number of people I am dealing with at any one time (including the person to whom I am speaking as well as any callers on hold).
(c) (3 marks) Find the steady-state average length of time it takes to make a phone call to me, including both time on hold and time spent speaking.
(d) (3 marks) Explain what the PASTA property is. Is it applicable to this queue? Why, or why not?
3. Suppose (Xn , n > 0} is a birth and death chain with state space S = (0, 1, 2, . . . , N} and transition probabilities given by
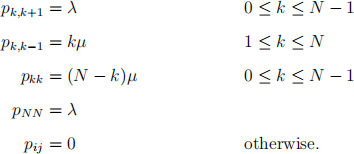
where λ, µ > 0, and λ + Nµ = 1. This is a version in discrete time of a queue with N servers, and no waiting room, where arrivals who find the queue full and all servers busy, leave immediately without entering. Thus N is the maximum number of people in the system at any one time.
(a) (3 marks) Write down equations that the equilibrium distribution satisfies.
(b) (6 marks) Obtain an expression for the equilibrium distribution for this chain.
(c) (3 marks) Suppose this chain begins with X0 chosen at random according to the equilibrium distribution. What is the expected number of upward transitions (births) in the sequence X0 , X1 , . . . , Xn ?
(d) (3 marks) This is a discrete time version of a continuous time model that is sometimes used to model the occupancy of an intensive care unit (ICU). Comment briefly on any assumptions that this model makes that might not be realistic (2 good points here are sufficient).
4. The arrival of fans at a rock concert can be modelled as follows. Start with a Poisson process of rate 10 per minute; let each Poisson event represent the arrival of a group of fans. A group contains
1 fan, with probability 0.2,
2 fans, with probability 0.3,
3 fans, with probability 0.2,
4 fans, with probability 0.2,
5 fans, with probability 0.1,
independently of its arrival time. Find the probabilities that:
(a) (3 marks) No 5-person groups arrive in the first minute;
(b) (3 marks) The time between 2 arriving groups is between 5 and 10 seconds;
(c) (3 marks) There are no arrivals at all in a 30-second period;
(d) (3 marks) The number of fans arriving in a 30-second period is at most 3.
5. A continuous-time Markov chain with state space S = (1, 2, 3, 4} has transition rate matrix
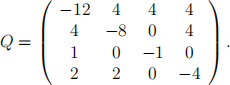
(a) (2 marks) Draw the transition diagram for this chain.
(b) (3 marks) If the chain is in state 1, what is the distribution of the time until the next transition?
(c) (3 marks) If the chain is in state 1, what is the probability that its next transition is to state 4?
(d) (3 marks) Write down the global balance equations for the chain. (e) (3 marks) Write down the local balance equations for the chain.
(f) (2 marks) Show that the chain’s steady-state distribution is given by π = (![]() ,
, ![]() ,
, ![]() ,
, ![]() ). (g) (2 marks) Is the chain time-reversible? Explain why or why not.
). (g) (2 marks) Is the chain time-reversible? Explain why or why not.
2023-06-08