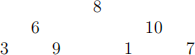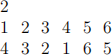CS234 Data Types and Structures

Assignment 4 (version 0)

        This problem set has a total of 3 problems on 5 pages. It covers Modules 8 (Q1) & 9 (Q2) & 10 (Q3). It will be marked out of 14, and accounts for 14% of the overall grade. Solutions should be submitted to MarkUS by 2am Friday August 6, 2021.

1. (3 points)

For this question we will be dealing with Min Heaps. That is, in a heap ordered tree, every node’s key is less or equal to the keys of its children, and the minimum is at root.

Consider a complete binary tree with height 3, with keys on the three levels, in order, as:

(so the left/right children of 8 are 6 and 10, the left/right children of 6 are 3 and 9, and the left/right children of 10 are 1 and 7)

(a) (1 point) give the result of running heapify on this tree, while going right-to-left on each level. That is, we try to bubble down up 10 first.

(b) (1 point) give the result of inserting π into the heap resulting from part (a). before you do this, please make sure your tree from part (a) satisfies the heap property

(c) (1 point) give the result of performing a Delete-Min on the resulting from part (b). Note that when doing delete-min, the min is first swapped with entry at the most recently inserted leaf. Again, please check to make sure your that your starting tree satisfies the heap property.

2. (3 points) Code https://dmoj.ca/problem/cco07p2.

This problems askes to find a pair of snowflakes that are the same, among n snowflakes provided in the input. Each snowflake is a 6-tuple of numbers, all non-negative. They can undergo rotations:

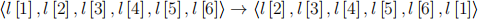
and flips:

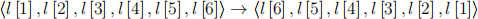
and two snowflakes are identical if the 6-tuple of one can be transformed into the 6-tuple of the other via a sequence of rotations and flips.

For Assignment 1 Question 5, you were asked to check if a particular pair of snowflakes are identical. Now we want to find a pair of identical snowflakes among n snowflakes in O(n log n) time or better. (the big-O is hiding a factor of 12).

Specifically, you should read input of the form of:

● Line 1: the number of snowflakes.

● Line 2 to n + 1: six numbers per line, the 6-tuple of a snowflake.

Then output ‘Twin snowflakes found.’ if there is a pair of identical snowflakes, or ‘No two snowflakes are alike.’ otherwise.

For example, for the input:

the output should be

Twin snow flakes found .

Your implementation should run with 15 seconds and use at most 1GB of memory. The test-data on MarkUS (and also DMOJ) can be downloaded at https://cs.uwaterloo.ca/~x2fang/files/a04q2_data.zip.

Note that the intention of this problem is to have you be a user of either the dictionary or list structures in Python. You should not be implementing your own dictionary/hash tables for this problem.

Approaches that we are aware of are:

● Store all previous snowflakes, and check whether flips/rotations of new ones are same as any of them. For this, Python’s built in dictionary data structure (set) is very useful, but you need to make snowflakes comparable first. There are two ways of doing this:

– Concatenate them into strings, with a separator symbol, e.g. ‘$’.

– Treat 6 the arms as the digits of a base number, aka, hash each snowflake to the number

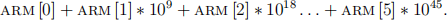
Richard’s code using this approach, that puts all 12 different rotations/flips of each snowflake into a set takes 2.6s max on DMOJ, the version that puts only 1 version into the set, and searches for all 12 rotations/flips of each new snowflake takes 2.4s max.

● Translate every snowflake into the lexicographical minimum representation (out of all 6 × 2 equivalence classes, find the minimum one when viewed as a 6-tuple). Then look for a duplicate in this list, either by sort or set. Richard’s implementation based on this approach, using sort on list, takes 2.6s max.

You may also use any code you wrote, or even the we provided in the solution, for the snowflake class from Assignment 1 Question 5.

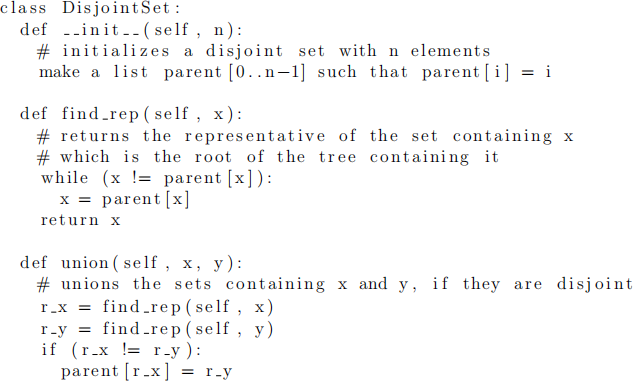
3. This question goes into more details on the Disjoint Set ADT introduced in Module 10b. However, we will work with a slightly modified version whose initializer takes the number of initial sets, and all sets are indexed by integers. This allows use of lists instead of sets (for faster runtime), and also omits the Add Set command. Specifically, the operations are:

● Create(n): initialize to n sets, each containing one element (integers from 0 to n − 1).

● Find Rep(x): finds a data item that serves as representative of set containing x.

● Union(x, y): if x and y are in different sets, combine the sets containing them.

This data structure is implemented as a tree, but only with parent pointers:

● The representative element is the root of the tree, and is extracted by following the pointers.

● When unionining x and y, we first find the root of their respective trees (by following parent pointers just as above), and . If they are different, we connect the two trees by setting the parent pointer of to (or vice versa: set parent of to ).

A pseudocode of this data structure is given below for reference. Note that an implementation trick here is to set the parent of the root node to itself.

(a) (3 points) Show that this implementation using only parent pointers can also support the Size(x) operation, which returns the size of the set containing x. Specifically, we still don’t keep children pointers/lists, but instead maintain an additional list size[x] that tracks the size of the subtree rooted at x. The difficulty here is to maintain these values as roots are connected during the Union operation.

You should describe how to:

● modify the constructor,

● modify the Union(x, y) operation,

● implement the Size(x) operation.

Also briefly justify that your data structure takes O(n) time per operation, where n is the total number of elements in all the sets.

(b) (3 points) Code a solution that solves Subtask 1 of https://dmoj.ca/problem/sac21ccp5. This problem is essentially the size-tracking union find described at the very start of this problem. You are to maintain n elements, labeled 1 . . . n initially all in disjoint sets, under q operations of one of the following two types:

i. Combining the sets containing u and v (if they are already in the same sets, do nothing).

ii. Return the size of the current set containing u.

The input format is:

● Line 1: two numbers, n, the number of elements, and q, the number of operations.

● Line 2 . . . q + 1: first a number in the range {1, 2}, the type of operation, followed by:

– if type 1, two numbers in the range [1, n], indices of the two elements,

– if type 2, one number in the range [1, n], index of a single element.

For the output, you should output, for each operation of type 2, the size of the set containing it.

For example, for the input

your output should be

because:

● For the first query, 3 can only reach 3.

● For the second query, 1 can reach 1, 2, and 3.

● For the third query, 4 can reach 4 and 5.

For this part, your program should handle 1000 operations involving 1000 elements in 15s time/1GB memory. The testdata on MarkUS (corresponding to Sample and Subtask 1 on DMOJ) can be downloaded at https://cs.uwaterloo.ca/~x2fang/files/a04q3b_data.zip.

(c) (2 points) Now we try to make things faster, to O(log n) per operation. Consider the following way of making union find faster: when unioning two trees rooted at  and , if the size of is smaller than the size of , set the parent of to , otherwise, set the parent of to . It can be shown that this modification reduces the cost per operation to O(log n). Do either of the following (your grade will be the higher of the two parts, both of which are out of 2)

i. Give a justification of why union by size guarantees that all resulting trees have height O(log n). Recall from Module 5a that the height of a tree is the maximum length of a path between the root and some leaf.

ii. Code a solution for both Subtasks 1 and 2 of https://dmoj.ca/problem/sac21ccp5 (described in part (b)). Your program should handle 100000 operations involving 100000 elements in 15s time/1GB memory. The data on MarkUS/DMOJ can be down-loaded at https://cs.uwaterloo.ca/~x2fang/files/a04q3c_data.zip..