Question 1  [24 marks].

(a)  Give the Pr¨ufer code of the following tree.           [4]

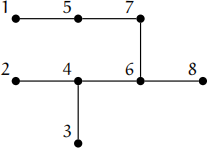
(b)  Give the degree sequence of the tree with Pr¨ufer code 6,4,3,2,1,6,4,6. Show your working.             [6]

(c) Draw a tree with degree sequence 3,3,2,2,1,1,1,1.                [2]

(d)  Show that any connected graph with degree sequence 3,3,2,2,1,1,1,1 must be a tree.            [6]

(e)  Give an efficient algorithm that, for any sequence d1 ,d2 , . . . ,dn  that is the degree sequence of a tree, constructs a particular tree with that degree sequence. Explain briefly why the algorithm is correct and efficient.          [6]

Question 2  [22 marks].            Consider the network (G,w) with

V(G) = {u,a,b,c,d,e,f,g},

E(G) = {ua,ub,uc,ac,ad,af,bc,bg,cd,ce,df,eg,fg},  and

w(ua) = 6, w(af) = 1, w(df) = 4,

w(ub) = 3,

w(bc) = 1,

w(eg) = 6,

w(uc) = 1,

w(bg) = 5,

w(fg) = 1.

w(ac) = 4,

w(cd) = 1,

w(ad) = 2,

w(ce) = 1,

(a) Draw G.                                                                                                                         [2]

(b) Apply Dijkstra’s algorithm to (G,w) starting from vertex u. Give V(T) and E(T) after each iteration of the algorithm.      [10]

(c) For each v ∈ V(G), give the length of a shortest u−v-path in (G,w). Justify your answer.         [4]

(d)  Show that the tree T obtained in Part (b) is the unique minimum spanning tree of (G,w).     [6]

Question 3  [26 marks].     Consider the directed network (D,c) given by the      following drawing, where each arc e ∈ A(D) is labelled by its capacity c(e) and two vertices s and t have been identified.

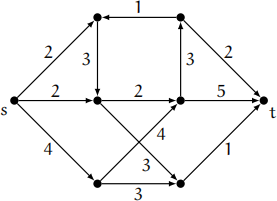
(a) Use the Ford-Fulkerson algorithm to find a maximum s−t-flow of (D,c). Draw the residual network after each iteration of the algorithm, and give the size of the maximum flow.       [14]

(b) Use a cut to show that the flow you have found is indeed a maximum s−t-flow of (D,c).              [6]

(c) If the capacity of exactly one of the arcs with capacity 4 was increased to 5, would this affect the size of a maximum flow? Justify your answer.                   [6]

Question 4  [28 marks].

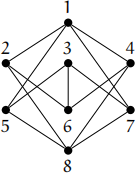(i)                     (ii)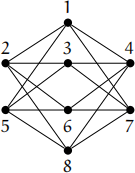           

Consider the bipartite graph G given by the following drawing, where each vertex is labelled with its name.

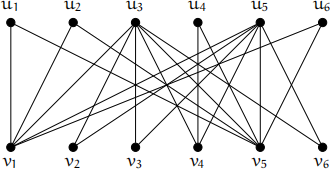
(b)  Show that M = {u2v5 ,u3v4 ,u5v2 ,u6v1} is a matching of G.

(c) Find a maximum matching of G. Show your working.

(d) Use Hall’s theorem to show that the matching you have found is indeed a maximum matching.