MTH6105: Algorithmic Graph Theory Main Examination period 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Main Examination period 2021 – May/June – Semester B
Online Alternative Assessments
MTH6105: Algorithmic Graph Theory
Question 1 [22 marks]. Consider the following network (G, w), in which each vertex is labeled with its name and each edge e e E(G) with its weight w(e).
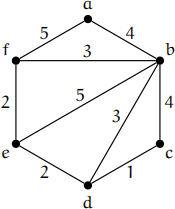
(a) Use Prim’s algorithm starting from vertex a to find a minimum spanning tree of (G, w). Show your working and give the minimum spanning tree and its weight. [10]
(b) Find another minimum spanning tree of (G, w). Show your working and give the minimum spanning tree and its weight. [4]
(c) Does there exist a minimum spanning tree of (G, w) that does not contain the edge de? Justify your answer. [4]
(d) Does there exist a minimum spanning tree of (G, w) that contains both of the edges bd and bf? Justify your answer. [4]
Question 2 [26 marks]. Consider a tree T in which the degree of each vertex is either 1 or 3. Let n = 1V(T )1.
(a) Show that n is even. [2]
(b) Show that T has 
+ 1 leaves. [6]
(c) Determine the number of distinct simple graphs G such that T is a spanning tree of G. Explain your reasoning. [6]
Call a graph G a tree-set if every connected component of G is a tree.
(d) For each of the following graphs, determine if the graph is a tree-set. Justify your answer. [6]
(i) The graph G1 with V(G1 ) = {v1 , v2 , v3 , v4 , v5 , v6) and E(G1 ) = 0
(ii) The graph G2 with V(G2 ) = V(G1 ) and E(G2 ) = {v1v2 , v2v4 , v2v6 , v4v6)
(iii) The graph G3 with V(G3 ) = V(G1 ) and E(G3 ) = {v1v5 , v2v6 , v3v4 , v5v6) Now consider an arbitrary graph G.
(e) Give a polynomial-time algorithm to determine whether G is a tree-set. Show that the algorithm is indeed a polynomial-time algorithm. [6]
Question 3 [24 marks]. Consider the following digraph D, in which each vertex is labeled with its name.
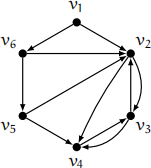
(a) Determine the strongly connected components of D. Show your working. Now consider the directed network (D, w), where w : A(D) → R with
w(v2v3 ) = 1,
w(v4v3 ) = 1,
w(v6v5 ) = 1.
presence of negative weights. Illustrate this fact by giving vertices u, v e V(D)
such that Dijkstra’s algorithm fails to find a shortest directed u−v-path in
(D, w). Explain your reasoning. [6]
(c) Use the Bellman-Ford algorithm to find a shortest directed v1 −v3-path in (D, w). Show your working. [12]
Question 4 [28 marks].
(a) For each of the following graphs, state if the graph is bipartite or not. Justify
your answer.
(i)
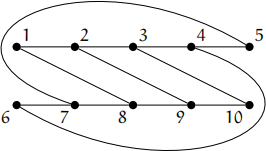
(ii)
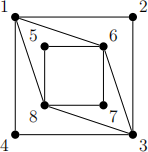
(iii)
Now consider the bipartite graph G with
V(G) = {u1 , u2 , u3 , u4 , u5 , u6 , v1 , v2 , v3 , v4 , v5 , v6)
E(G) = {u1v2 , u1v4 , u2v1 , u2v2 , u2v3 , u2v4 , u2v5 , u2v6 , u3v2 , u3v4 , u4v2 , u4v3 , u4v4 , u5v2 , u5v4 , u6v1 , u6v2 , u6v4 , u6v5 , u6v6).
(c) For each of the following sets, state if the set is a matching of G or not. Justify
your answer. [ ]6
(i) M1 = {u1v2 , u2v1 , u5v2 , u6v4)
(ii) M2 = {u1v2 , u2v1 , u3v3 , u4v4)
(iii) M3 = {u1v4 , u2v2 , u4v3 , u6v5)
(d) Find a maximum matching of G. Show your working. [10]
(e) Show that the matching you have found is indeed a maximum matching. [4]
2023-05-28