MATH0026 EE 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH0026
Submit all four solutions.
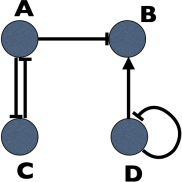
1. (a) Consider a system of four genes which express proteins A, B , C and D (see the figure). A inhibits B and C by means of n-mer An . C inhibits A by means of n-mer Cn . D represses itself but activates B by means of n-mer Dn . Assuming gene regulation according to the Hill equations, where n is the coefficient of cooperativity, derive the differential equations for the concentrations of A, B , C and D .
In your derivation assume that:
(i) The expression of B occurs with basal rate b. The expression of A, C and D has no basal rate.
(ii) The DNA molecule of gene A can be in 2 possible states, unbound: OAU , or bound with Cn : OAC . The expression of gene A occurs with the rate αAU OAU + αAC OAC , but can occur only when gene A is not bound with the repressor Cn . The same (with A instead of C) is valid for gene C .
(iii) The DNA molecule of gene B can be in 4 possible states, unbound: OBU , bound with Dn : OBD , bound with An : OBA , or bound with An and Dn : OBAD . The expression of gene B occurs with the rate αBU OBU +αBD OBD + αBA OBA +αBAD OBAD , but can only occur when gene B is bound only with activator Dn , and is not bound with the repressor An .
(iv) The gene D is an auto-repressor, and, hence, the expression of gene D occurs only, when it is not bound with the repressor Dn .
(v) The total number of DNA molecules is fixed and equal to N for each gene.
(vi) All rates for the production of An and Cn are equal to kd = 1, and they degrade with the rate k−d = 1. All rates for binding of DNA molecules with the transcriptional factors are kb = 1 and for unbinding k−b = 1.
(vii) Proteins A, B , C, and D degrade with rate γ = 1.
(b) Can this system function as a bistable switch? Are there any conditions for n?
(c) Assume now that transcriptional regulation occurs with delay τ . How will the Hill equations change in this case? Write down the new equations. What is the biological reason for the delay?
(d) Can this system function as a genetic clock? Are there any conditions for n or τ ?
(e) Explain what is the meaning of a Hill coefficient (a coefficient of cooperativity). Could it be non-integer? Why?
(f) In lectures we have considered a model of a genetic associative perceptron. Sketch the genetic network and explain briefly how this system works as an associative perceptron, showing responses to different stimuli.
(g) In lectures we discussed how intrinsic genetic noise can extend the memory of an association. Explain briefly a mechanism for this effect.
2. The Fitzhugh-Nagumo system of differential equations is the following:
 dv
dv
= bv - γw
dt
where f (v) = v(a - v)(v - B), 0 < a < 1 and B = 1.
(a) Consider a = 0.25, b = γ = 0.003 and Ia = 0:
(i) Find all equilibria of the system and classify them by linearising the system near each equilibrium
(ii) Graph the nullclines
(iii) Sketch a trajectory in the phase plane if the system starts below both nullclines, but beyond the second local maximum of f (v), at w = 0. How
would we refer to this typical dynamical regime?
(b) Now consider a = 0.25, b = 0.03, γ = 0.3 and Ia = 0:
(i) Find all equilibria of the system.
(ii) Graph the nullclines.
(iii) Classify each of the equilibria by the behaviour of the local vector field. (iv) Sketch the typical trajectories for the following starting points
A. Below the w-nullcline and below v-nullcline, in the region where v ≈ 0.6, w ≈ -0.1,
B. Above the w-nullcline and above v-nullcline, in the region where v ≈ 0.3, w ≈ 0.1.
(c) Consider a different model described by the equations:
![]()
![]() = v - - w,
= v - - w,
![]() = v + 2b,
= v + 2b,
dt
where b is a constant. By analysing the eigenvalues of the equilibrium points, find the values of b, for which the only attractor is
(i) a stable fixed point;
(ii) a limit cycle.
3. (a) Consider a bone which is square in cross-section, where a is the external edge of the hollow square, and b is the inner side (see the figure below). Find the area moment of inertia Ia,square around the neutral axis as a function of the angle θ . Compare it with the area moment of inertia Ia,cylinder of a bone that is a hollow cylindrer in a cross-section with the external radius a and the internal radius b. Is there any angle θ, for which the Ia,cylinder > Ia,square ?

(b) Consider the Kelvin model of viscoelasticity shown in the figure:

Find the equation describing the relation between the applied force F (t) and the response deformation x(t). Here c is the constant of the dashpot, k1 and k2 are constants of two springs, xT , x1(T) , x2(T) are the total length of the corre- sponding parts, xE , x1(E) , x2(E) are the length of these parts in equilibrium without force, and x, x1 , x2 are the deformations of these units (see figure). Use the
notation
![]() x 1 1
x 1 1
Suppose that bone described by the Kelvin model is deformed by a force F (t) defined as
F (t) = 3F0 (Θ(t) - Θ(t - τ )) + F0 (Θ(t - τ ) - Θ(t - 2τ )),
where Θ(t) is the Heaviside step function and F0 is a constant. Find the analytical expression for the response deformation x(t) and sketch it. The final expression should be written using Heaviside functions.
(c) In lectures we have discussed that a bone can be remodelled if a stress applied has changed direction. The adaptation to the new direction of stress can be improved if fluctuations are also applied. Explain briefly a mechanism of this
effect.
4. (a) Explain an experiment that clearly demonstrates that transporting oxygen by diffusion is only efficient at very short distances.
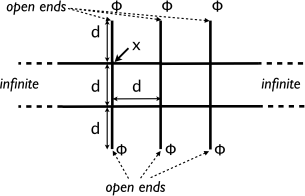
(b) Consider oxygen transport with uniform diffusion constant D = 1/2 and uni- form absorption rate µ = ν2 /2 within an infinite network with equally spaced nodes d apart along its entire length as shown in the figure below. The net- work consists of pipes of length d with free ends open to the outside, where the oxygen concentration is a constant Φ . Oxygen transport in the pipes is purely diffusive, i.e., there is no advection. Find the oxygen concentration x at the internal nodes in terms of Φ, defining carefully any other quantities that you need.
(c) Now consider oxygen transport with uniform diffusion constant D = 1/2 and uniform absorption rate µ = ν 2 /2 within a different network as shown in the figure below. After each pipe of length L the network branches into three pipes of the same length L, and this repeats indefinitely. Again there is no advection. At the beginning of the network there is an open end, where the oxygen concentration is a constant x. Find the expression for the concentration xn at nth branch. What is the value of xn if n → -? How does xn depend on L? Briefly explain your findings.

2023-05-22