MATH 103A Summer 1 2021

Homework 1

Instructions

One member of the group should upload your group submission to Gradescope. While sub-mitting they will be prompted to add the rest of the names.

Your homework must be typed. It is recommend that you submit early drafts to Gradescope so that in case of any technical difficulties, at least some of your work is present. You may update your submission as many times as you’d like up to the deadline.

Your assignments in this class will be evaluated not only on the correctness of your answers, but on your ability to present your ideas clearly and logically. You should always explain how you arrived at your conclusions, using mathematically sound reasoning. Whether you use formal proof techniques or write a more informal argument for why something is true, your answers should always be well-supported. Your goal should be to convince the reader that your results and methods are sound.

1. (15 points) Consider the three binary operations on the set {a, b, c, d} described by the tables below. Either show that these operations satisfy the conditions to be a group (you may skip writing out justification that it is associative), or show that it does not satisfy the conditions to be a group.

(a)

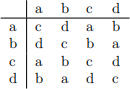
(b)

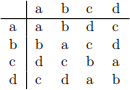
(c)

2. (12 points) For each of the following sets with a given binary operation, explain why they do not form a group.

(a) The real numbers under multiplication

(b) The positive integers under multiplication

(c) The integers under subtraction.

(d) The positive integers under addition

(e) The positive real numbers under taking geometric means (the geometric mean of two numbers x,y is )

(f) The integers under the operation ∗ given by x ∗ y := |x − y|

3. (25 points) A Latin square is an array in which each of n distinct symbols appears exactly once in each row and column.

(a) Prove that the table for the binary operation of any finite group (taken without the 1st row and column that provide the labels) form a Latin square

(b) We might be curious if the converse of the previous statement holds. That is, if the table of a (finite) binary operation forms a Latin square, does the binary operation have to form a group?

Consider a (finite) binary operation whose table forms a Latin square. For each of the properties that a binary operation is required to satisfy in order to form a group (associativity, has a 2-sided identity, every element has a 2-sided inverse), either prove that this property must hold for this binary operation, or give a counterexample to show that it does not need to hold.