Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Math 4446, Project 2

Compress the MATLAB files and project report into a zip (or tar, gz) file and upload to Canvas .  The report should be typed (eg.  by LATEXor MS WORD), with requested MATLAB codes and answers to questions .  Note  that this is not a group project and an honor code pledge must be included in the submitted report.  Acquiring  codes  and solutions from  any unauthorized source  (eg.  online source, solution manual,  or other students) is a violation of the  Virginia  Tech honor code .

1. Area enclosed by a smooth curve. Suppose we want to compute the area enclosed by a smooth curve based on some discrete points  {(xi; yi)} on that curve.   Matlab has a convenient function polyarea to compute the area of a polygon, but we want to do better than that. (i) Design a more accurate algorithm to compute the area based on what you have learnt in this course. Explain how it works.  (ii) Based on your algorithm, write a code with the following header. Your function should at least work for general convex regions and pass the accuracy test in problem 2 (a).  It is preferable (not mandatory) that your code has no constraint on the parity of n and also work for non-convex regions. If needed, you may utilize the builtin matlab functions that you have learnt in this course to perform interpolation or numerical integration. Attach your code to the report.

2.  Code validation. Use your code to compute the area of a tilted ellipse based on n points

where i = i. The exact area of this ellipse is 6 .

(a) For n = 10, polyarea outputs 17.6336, with an absolute error 1.2160. Test your function,

and make sure the error is at least 10 times smaller than that of polyarea.

(b)  Repeatedly double n, tabulate the errors of polyarea and your function, and find the corresponding orders of accuracy. Try to make sense of the observed orders of accuracy.

3.  Single vortex test.  In the community of computational fluid dynamics (CFD), when people design a new algorithm for incompressible interfacial flows, they usually need to demonstrate the mass-conservation property by computing the deformation of a circular drop under a swirling flow.  In this test case, the initial interface is a circle centered at (0:5; 0:75) with a radius 0.3. The incompressible velocity field is given by

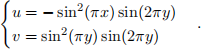
The interface shapes at different times are given in the figure below.

Theoretically, the area enclosed by the interface is a constant, i.e., it is always 0．152 π .  We can use a simple technique to track the interface: markers (the symbols О along the interface). Those markers are advected by the velocity field and the position can be obtained by solving an ODE system using the Runge-Kutta method (to be discussed near the end of this semester). From the marker positions, we can reconstruct the interface.

(a) Use 32 markers to compute the area of the drop at t = 0．1.  The marker positions can

be generated using the code markers Euler .m on canvas with Nm=32, t end=0 .1, and dt=0 .0001. Compare the result of your function with that from polyarea.

(b)  (Optional) At t = 0．5 and later, the drop shape is no longer convex. If your code also

works for non-convex regions, compute the areas at t = 0．5﹐ 1．0﹐ 2．0﹐ 3．0 using 32 markers. Provide discussions on the results.

(c)  (Optional) The code markers Euler .m uses Euler’s method to update the position of markers, which is not very accurate.  Thus we have to use very small dt to achieve a reasonable accuracy.  Replace Euler’s method with a more accurate method that you have learnt from this course,  eg.,  the classical 4-stage Runge-Kutta method  (RK4). Name the code as markers RK .m.  Repeat (a) with marker positions generated by your new code.  Try different time step size dt and find the dt that can achieve a similar accuracy (demonstrated by the error of drop area) as Euler’s method in (a). Comment on these two methods (Euler and RK of your own choice).