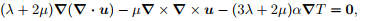MATH35021: Coursework
Linear (uncoupled) thermoelasticity
In the standard formulation of elasticity the stress(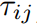 ) is a function of the strain (
) is a function of the strain ( ) only. Hence, for an isotropic, homogeneous, linear elastic material, in the absence of any pre-stress, the constitutive law is
) only. Hence, for an isotropic, homogeneous, linear elastic material, in the absence of any pre-stress, the constitutive law is
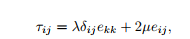
| where δij is the Kronecker delta and λ and µ are the Lam´e constants. |
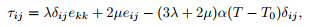
where α is the rate of thermal expansion, T (x) is the temperature field and T0 is a constant reference temperature.
1. Understanding the constitutive law (4 marks)
(a) Use equation (2) to show that the body is unstressed when it is unstrained and the temperature is T0.
(b) Find the strain tensor that leads to a state of zero stress at constant temperature type of physical deformation is represented by this strain tensor?
2. Governing equations (displacement form) (4 marks)
Use the definition of strain and the equations of motion from the lecture notes with the thermoelastic constitutive law (2) to deduce the thermoelastic equivalent of the steady Navier–Lam´e equations in the absence of any body forces:
where u is the displacement vector.
3. Cooling a pipe (12 marks)
A circular cylindrical pipe of a linear elastic material with constitutive behaviour described by equation (2) has undeformed inner radius a and outer radius b. The pipe is full of stationary cold water maintained at a temperature T1 and the external air temperature is T0. The inner and outer walls of the pipe are stress free.
(a) Find the temperature field within the pipe walls, assuming that the temperature field obeys a steady diffusion equation,
(a) Find the temperature field within the pipe walls, assuming that the temperature field obeys a steady diffusion equation, ∇2T = 0, and is a function only of r, the distance from the central axis of the pipe.
(b) Hence, use equation (3) to find the displacement of the pipe in the special case when a = 1, b = e (Euler’s number, i.e. 2.71...), T0 = 1 and T1 = 0. State clearly any simplifying assumptions made.
(c) Produce a graph of the temperature distribution and displacement field throughout the pipe for a = 1, b = e, T0 = 1, T1 = 0, λ = 2, µ = 1, α = 1. Explain the result physically.
You may use the results that in cylindrical polar coordinates (r, θ, z),
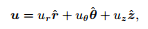
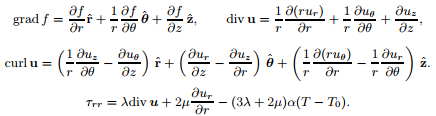
2019-11-23