Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

MAST30011 Graph Theory 2023

Assignment 1

Due 23:59pm Monday 17 April 2023

1. In the following graph, [10 marks]

(a) give an example of a longest trail

(b) give an example of a longest cycle

(c) give an example of a longest path

(d) list all induced subgraphs which are paths of length 4

(e) list all bridges of the graph

(f) write down the degree sequence of the subgraph induced by {b, c, d, e, g} (g) give the diameter of the graph

(h) give two distinct automorphisms of the graph which are not the identity map from the vertex set to itself.

You are not required to justify your answer to any part of the question.

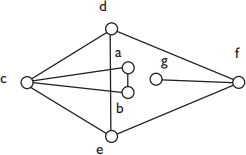
Figure 1: Question 1

2.    (a) Show that there is no tree with order 100 such that every vertex has degree 1 or 5. [3 marks]

(b) Prove that, if G is a connected graph in which every vertex has even degree,

then G has no bridges. [3 marks]

3.    (a) Prove that, if G is a connected graph with minimum degree at least 2, then G contains at least one cycle. [3 marks]

(b) Using the result from (a), prove the following: If G is a (possibly disconnected) graph with minimum degree at least 3, then G contains at least two distinct cycles. [3 marks]

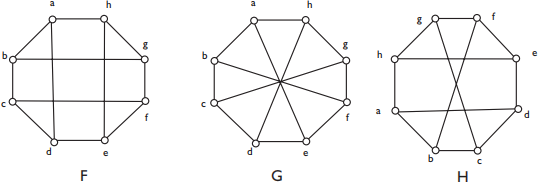
Figure 2: Question 4

5. Let G be the following weighted graph, where the number next to each edge is the weight of the edge.

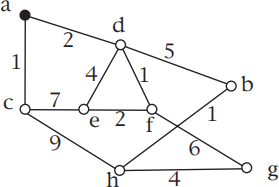
Figure 3: Question 5

Apply Dijkstra’s algorithm to find the distance from a to all other vertices of G. State what the labels of vertices are when each new vertex is chosen to be added to the set S . Draw the tree of shortest paths obtained from your implementation of the algorithm, and explicitly give the shortest path from a to every other vertex obtained from this tree. [6 marks]

6. Suppose that G G and that n = |V (G)| = 4k + 1 for some integer k > 1, where G is the complement of G.  Suppose that the degree sequence of G is d1  > d2  > · · · > dn .

(a) Prove that di + dn −i+1  = n . 1 for each i = 1, 2, . . . , n. [4 marks]

(b) Use (a) to prove that G has at least one vertex with degree (n . 1)/2. [2 marks]