Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

CO 250 Winter 2023: Assignment 8 problems

Due: Wednesday March 29, 5:00pm EDT

Assignment problems.

A8-1. Geometry of optimality

Consider the following linear program (P) where c is an unknown vector.

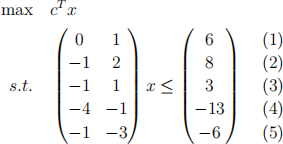
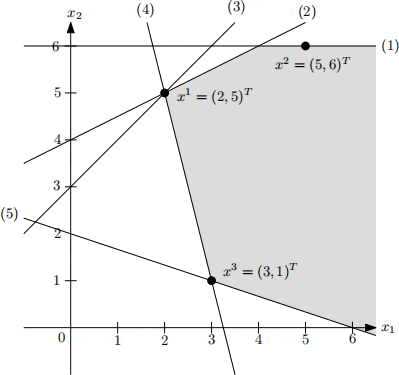
(a) Consider the three points x 1 = (2, 5)T , x2 = (5, 6)T , x3 = (3, 1)T . For each of these points, determine its cone of tight constraints. Sketch the cone around the point on the diagram.

(b) Suppose c = (−2, α) T . Determine (with proof) all possible values of α for which x 1 is an optimal solution.

(c) Is there a vector c for which both x 1 and x 3 are optimal? If so, derive all such vectors algebraically using cones. If not, explain why not.

(d) Is there a vector c for which both x 1 and x 2 are optimal? If so, derive all such vectors algebraically using cones. If not, explain why not.8jJUrTR5xXP3Vw

A8-2. Farkas’ Lemma

(a) Let A be an m×n matrix, and b ∈ R m. Prove the following variation of Farkas’ Lemma using duality.

Exactly one of these two conditions holds:

i. There exists a vector x ∈ R n where Ax ≤ b.

ii. There exist vectors y ∈ R m where y ≥ 0, AT y = 0 and y T b < 0.

(b) Suppose A has rank n. The goal of this problem is to show that if Ax ≤ b is infeasible, then there exists a subsystem of at most n + 1 constraints that is infeasible.

For example, when n = 2, the following system on the left with 5 constraints is infeasible. But we can find 3 of these constraints such that the system on the right with just these 3 constraints is infeasible.

Follow these steps in your proof (each step is pretty short):

i. Consider the system AT y = 0, bT y = −1, y ≥ 0, we denote it by (S). Explain why (S) is feasible. (Hint: Use part (a).)

ii. The system (S) is in standard equality form. We can rewrite the main constraints as

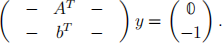
Show that the coefficient matrix has rank n + 1. (Hint: Show that b is linearly independent from the column vectors of A.)

iii. Explain why (S) has a basic feasible solution.

iv. Explain how you can remove some columns from (S) and their corresponding vari-ables to obtain another system (S′ ) with at most n + 1 variables, such that (S′ ) is feasible.

v. Use (S′ ) to conclude that there is a subsystem of Ax ≤ b of at most n+1 constraints that is infeasible.

A8-3. Shortest paths algorithm

(a) Perform the shortest path algorithm on the following graph where each edge e is labelled with its length ce. For each iteration, record all details including the cut you are considering, the slack of each edge in the cut, the width assignment of the cut, and the new tight edge. At the end of the algorithm, produce a shortest s, t-path and a set of width-assignments, and prove directly that they are optimal for the primal and dual LPs for the shortest path problem using the weak duality theorem.

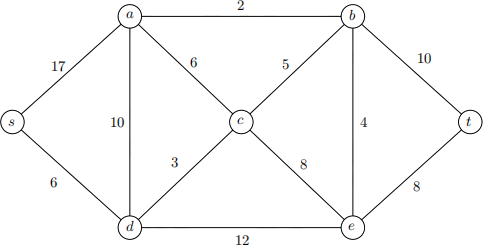
You may choose to use the worksheet provided on LEARN for your solution.

(b) For the vertex a, there is a path from s to a that consists of only the tight edges. State what this path is, and prove that this is a shortest s, a-path using the Complementary Slackness Theorem.