1.  Consider a mobile company that wants to connect wireless clients to base stations. Further suppose that each base station has a capacity of C clients. A client can connect to a base station only if the base station set is less than or equal to distance r away. Given a collection of base stations, wireless clients and the geographic location of base stations and wireless clients, design a method to determine an assignment of clients to base stations such that the number of clients serviced is maximized.

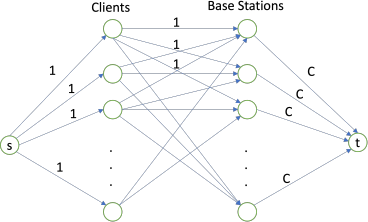
We can formulate this as a max-flow problem in a bipartite graph. Create a bipartite graph G(U,V,E) where U represents the set of clients We let ui be the node corresponding to client i, vj  corresponding to the jth base station. E = (ui,vj  represent an edge directed from client ui  to base station vj  iff ui is within distance r from vj . Create a super source and connect to ui , Ai and connect vj , Aj to t. Let all edges have capacity 1 and let the edge from vj  to t have capacity C .  This capacity will ensure that no base station will get more than C client. Finding the maximum flow in this graph will give an optimum assignment. 

2.  There are n doctors that need to be scheduled for duty in a hospital during holiday periods. There are m vacation periods (Thanksgiving, Christmas etc.)  each of period pi .  However, there must be at least one doctor on call at the hospital every day during the vacation period.  Each doctor Di specifies the set of vacation days Wi  that he can work. How will you determine a schedule such that each doctor is not working more than c days in any vacation period.

Again construct a flow network using a variation of a bipartite graph G = (V,U,E) where U represents the doctors, V the holiday days and an edge between ui  and vj  if the doctor ui  can work on holiday vj . Each edge has capacity 1. However we need to make sure that no more than c days are scheduled for every doctor.  So we add a third layer of nodes in between U and V such that for every holiday period h and for every doctor there is a node hi  and now every node corresponding to a doctor ui  is connected to hi  with capacity c and every node hi  is then connected to all the nodes corresponding to the days in the holiday period h with capacity 1. Add a super source s with edges to each doctor and of unbounded capacity and a super sink t with edges from vj  to t with capacity lower bound of 1 and upper bound of 1.

3.  Describe the proof of Hall’s theorem discussed in class for a bipartite graph  G  =  (U,V,E).   In particular, in the induction step show that if there is a subset S ⊆ U with neighbor set N(S), where |N(S)| = |S| then S and T satisfy the hypothesis of the the theorem, i.e., for every subset in S(or

T) the neighborhood set is of size greater than or equal to S (or T).

When |A| = 1, then an A-perfect matching is trivial.  When  |A| > 1, we can consider x ∈ A and y ∈ B

Next, for any vertex x ∈ A it must have at least one neighbor y ∈ B .  We can try to pair x and y and find a matching of size |A| − 1 in the graph induced by A − {x},B − {y}.  Such a matching will not be possible if there is some set S in the induced graph where S < N(S) (Observe that the total neighborhood size of A has only decreased by 1, invalidating Hall’s condition.)  Therefore, S has exactly |S| neighbors in B .

Let T denote the neighborhood of any such S in B, i.e., |S| = |T|. Extract S and T and Let B\  be the induced graph (B is the original graph.)  B\  is definitely smaller in size than B , and therefore, there exists a matching for each vertex of S to a vertex in B .  For any set S\  = A / S .  Since S has |T| neighbors in B , S\  must have at least |S\ | neighbors in B / T.

Ref:  https://homes.cs.washington.edu/ ˜anuprao/pubs/CSE599sExtremal/lecture6.pdf

4.  Show that y(θ) = θx + (1 − θ)y, 0 ≤ θ ≤ 1 represents all the points on the line segment defined by two endpoints x and y . This is true in Rd  for any dimension d.

All points on the line segment can be expressed in terms of the vector x + t(y − x) where 0 ≤ t ≤ 1.

Manipulating the expression in the question, we have y(θ) = y + θ(x − y), 0 ≤ θ ≤ 1, which matches the definition.

5.  Show that the following sets are convex:

(i) Lines and Line segments in Rd .

Using parametric definition of a line:  A line is defined by a point p,  a vector v  and is the set {y = p+αv}, for any α . Given y1 = p+α1v and y2 = p+α2v on the line consider z = θy1 +(1−θ)y2 .

z = p + (α1v)(θ) + (α2 )v(1 − θ)

or z = p + (α\ )v where α\ = (α1 θ + α2 (1 − θ))

(ii) Ellipsoids in Rd .

Ellipsoids in d dimensions are defined by

(x − c)T B(x − c) ≤ 1

Note that B can be expressed as AT A and thus the above is equivalent to ||(x − c)tA||2  ≤ 1.  Then checking for z = θx + (1 − θ)y gives

(z − c)T B(z − c) = θ  (x − c)2T B(x − c) + 2θ(1 − θ)(x − c)T B(y − c) + (1 − θ) (y − c)2T B(y − c)

≤ θ2 + (1 − θ)2 + 2θ(1 − θ)((x − c)A)T (A(y − c))