PHYS3040/PHYS7042 Quantum Mechanics II Module 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
PHYS3040/PHYS7042 Quantum Mechanics II
Module 1
Homework Problem - Due: 5pm 10/03/23
Part A (grade: 1-5)
1. Consider the orthonormal basis {|0⟩, |1⟩} for the Hilbert space of dimension N = 2. Take a vector state |w〉 = 
(i|0⟩ + 2|1〉). Using Dirac notation (the properties of kets, bras, and scalar product):
a) Show that |w〉 is normalized, i.e. 〈w|w〉 = 1.
b) Write down a decomposition of |w⟩ in the new basis {|±⟩ = 
(|0⟩ ± |1⟩)}.
2. Take the projection operators 
0 = |0〉〈0| and 
1 = |1〉〈1|. Find the matrix representation for these operators. Check that 
0 = 
0 , 
1 = 
1 and 
0 + 
1 = 1 using the matrices.
3. Consider operators of z and x components of spin- 1/2 operator:
a) Show that 
z and 
x don’t commute.
b) Check that | + x ⟩ = (| + z⟩ + | − z⟩)/√2 is an eigenstate of 
x if |±z ⟩ are eigenstates
c) What would be the outcomes of measurement of z-components if the system is prepared in | + x ⟩ before the measurement? What would be the corresponding probabilities to get these outcomes?
d) Calculate the expectation value ⟨
z ⟩ and its dispersion ΔSz ≡ ((
z(2)) − ( 
z )2 )
.
4. Suppose the Hermitian operator  corresponding to an observable A has two eigenstates |a1 〉 and |a2 〉 with non-degenerate eigenvalues a1 and a2 , respectively.
a) Write down the matrix representation of  in the basis of |a1 〉 and |a2 〉 .
b) Show that  can be written in the form  = a1 |a1 〉〈 a1 | + a2 |a2 〉〈 a2 |
c) Use Taylor series for some function f(x) = c0 + c1x + c2x 2 + ⋯ to evaluate f(Â )|a1 〉 and f(Â )|a2 〉 .
d) Evaluate the matrix representation for f(Â ) in the basis of |a1 〉 and |a2 〉 .
5. Consider two commuting operators  and 
: [Â , 
]=0. Suppose |X〉 is an eigenstate of  :  |X〉 = a |X〉 , where eigenvalue a is not degenerate. Show that |X〉 then it is also an eigenstate of 
.
Part B (Advanced: grade +0,+1,+2)
1. Write the matrix representation for 
0 and 
1 in the basis {|±⟩ = 
(|0⟩ ± |1⟩)} and check
that 
0 = 
0 , 
1 = 
1 and 
0 + 
1 = 1.
2. We have an uncertainty relation for operators  , 
and 
: (ΔϕÂ )(」小 
) ≥ 
|〈
〉 小 |, if
[Â , 
] = i 
. Take Pauli matrices: ox = ( 1 0) , oy = ( i 
i) and oz = ( 0 
1) and
find a state (analytically, numerically or by trial-and-error) for which the Heisenberg
inequality becomes equality. Draw this state on the Bloch sphere and explain why this is
the case.
The following question is compulsory and assessed for PHYS7042 students; it is optional and unassessed for PHYS3040 students.
3. Locate and briefly describe (about 300 words) some recent research that uses some of the concepts or techniques discussed in this module. Points to cover include:
a. What motivates the research? (i.e., the background)
b. What specific scientific question did the research aim to answer? (i.e. the problem to be solved)
c. What key strategy, techniques or technology did the researchers use?
d. What is the main result?
e. What is the significance of the result? (i.e., the outcome)
Although you may use commentary sites below to find recent research, make sure you locate and cite the original research article.
Helpful commentary sites:
Extra Tutorial Problems (not assessed)
1. Prove that if A者 is a linear operator and {|n〉} is complete orthonormal basis then (A者t)nm = A者m(*)n.
2. Prove that 
= e一i a 
is unitary ifA者 is Hermitian and a is a real number. Prove or disprove that any unitary operator can be represented in this form.
3. Consider two commuting operators A者 and 
: [A者, 
]=0. Suppose |X〉is an eigenstate of A者: A者|X〉= a|X〉, where eigenvalue a is degenerate. Is |X〉also an eigenstate of 
?
4. Prove that the necessary and sufficient condition for |p〉to be an eigenvector of a Hermitian operator is that the dispersion 」小A is zero.
5. Explain the physical meaning of dispersion.
6. Derive the Heisenberg inequality (A中A者)(」小 
) ≥ 
|〈
〉小 | for operators A者, 
and 
if one has [A者, 
] = i 
.
Consider an analogue of the Elitzur-Vaidman bomb testing problem formulated for the Stern- Gerlach experiment show in Fig. 1. The unpolarized silver atoms are sent through three SG filters oriented along z, x and z axes, respectively. The middle filter contains the black box in the lower arm of the filter. The box may contain either live or dud bomb. The bomb has a sensor such that each silver atom will trigger the bomb. The dud bomb will just let the particle pass it without interacting with it.
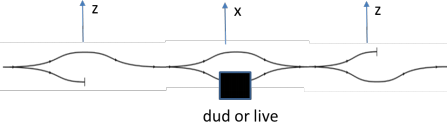
Figure 1 The analogue of the Elitzur-Vaidman bomb testing problem formulated for the Stern- Gerlach experiment
a) Evaluate the state of the atom before and after the middle SG filter for the case of the live and dud bomb.
b) If N particles are sent to the input how many particles will exit the last device if the box contains the dud bomb?
c) If N particles are sent to the input and the box contains the live bomb, how many particles will trigger the bomb?
d) If N particles are sent to the input and the box contains the live bomb, how many particles will NOT trigger the bomb?
e) How many of these particles will exit the last device?
f) If you observe that the particle exits the device what will you conclude about the content of the box?
2023-03-11