Math 4547 Midterm
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 4547 Midterm
Due Friday March 10, 2023
Instructions: You may use textbooks and course notes on this exam. You may also exchange ideas with others in the class. However, all submitted so- lutions must reflect your own understanding and evidence to the contrary (in- cluding having a solution which is identical to a solution from another source, or a solution which is identical to another student’s solution) will be consid- ered cheating and will result in a automatic failure and possible disciplinary procedure.
All solutions must include rigorous proof for full credit. Any result covered so far in lectures or in homework may be used freely (with citation) unless stated otherwise.
1. In class, we showed that Q is dense in R. Improve this result by showing that for any real numbers a, ∈ R with a < b, there are infinitely-many distinct rational numbers {qn : n ∈ N} such that a < qn < b for all n ∈ N.
2. Let {Ai | i ∈ I} be a (possibly infinite) collection of nonempty, bounded subsets of R. Let αi = supAi for each i ∈ I . Compute sup (ni∈I Ai ) in terms of {αi | i ∈ I}. A complete solution requires proof.
Remark: The following is not required for this problem, but you can also compute the infimum of the union in terms of the infima of each Ai . Similar results hold for the supremum and infimum of the intersection of a collection of sets, provided that the intersection is non-empty.
3. Using only the definition of convergence, prove that
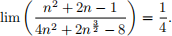
If you use the Algebraic Limit Theorem or any other theorem about convergence of sequences, you will not receive credit for your solution.
4. Let (an ) and (bn ) be sequences such that lim(an ) = +∞ and (bn ) is bounded below. Prove that lim(an + bn ) = +∞ .
5. Consider the sequence
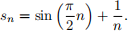
Compute limsup(sn ) and liminf(sn ). Calculate the set of subsequential limits of (sn ). A complete solution requires proof.
6. In class, we showed that Q is countable. Let s : N → Q be a bijection and let (sn ) be the sequence corresponding to s (i.e., sn = s(n) for all n ∈ N). Said another way, (sn ) is an enumeration of Q because every rational number occurs precisely once in this sequence. Prove that the set of subsequential limits of (sn ) is the entire extended real line R n {−∞, +∞}.
7. Let (an ) be a decreasing sequence of non-negative real numbers. Prove that if z an converges, then lim(n · an ) = 0.
8. Prove the following statement: If z an converges absolutely and (bn ) is a bounded sequence, then z an bn converges absolutely.
Throughout this course, we have proved various theorems which are related to the non-existence of“gaps”in R including the Nested Interval Property (HW2 #8), the Monotone Convergence Theorem, the Bolzano-Weierstrass Theorem, and the Cauchy Criterion (for sequences). Each of these was proved directly or indirectly by assuming the Axiom of Completeness. However, it turns out that each of these theorems is logically equivalent to the Axiom of Completeness, meaning we could have just as easily taken one of the above theorems as an axiom at the beginning of the class and used it to prove AoC and the other results on this list as theorems.
In the following problems, you will show that this is true by assuming one of the above theorems holds and proving that AoC holds. In these problems, you may assume that the 14 of an ordered field1 hold, and you may use any result which relies only on these axioms. However, in these proofs you may not invoke the Axiom of Completeness or any theorem which we proved using the Axiom of Completeness, since that would make your argument circular.
9. Assume the Nested Interval Property holds for R and prove that the Axiom of Completeness holds. In other words, you may assume that any nested sequence of closed bounded intervals I1 ⊇ I2 ⊇ I3 ⊇ · · · , the intersection U
In 
∅. Prove that for any nonempty set A ⊂ R which is bounded above has a least upper bound in R.
10. Assume the Cauchy Criterion for sequences of real numbers and prove the Axiom of Completeness. In other words, assume that for all sequences of real numbers, the sequence is Cauchy if and only if it converges to a real number. Use this to prove that any nonempty set A ⊂ R which is bounded above has a least upper bound in R.
2023-03-06