CHBE 692 - Applied Mathematics HOMEWORK ASSIGNMENT #4
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CHBE 692 - Applied Mathematics
HOMEWORK ASSIGNMENT #4
Due: Sunday, 26 February by 11:59 pm.
Question 1 - 30 points
Consider the diffusion of particles characterized by the diffusion equation
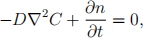
with no sources in a cubical box of size L×L×L, defined by 0 ≤ x,y,z ≤ L. No particles are allowed to escape, so that all boundaries, at x,y,z = 0 or L, are reflecting with vanishing normal component of flux.
(a) Explain why all solutions for C(r,t) can be described in the form
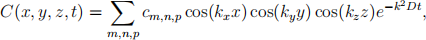
where kx = mπ/L, ky = nπ/L, kz = pπ/L and k2 = kx(2) + ky(2) + kz(2) . What values of m,n,p are possible here? Find the solution for an initial distribution of particles C(x,y,z,0) given by C = 1 for 0 ≤ x ≤ L/2 and C = 0 for L/2 < x ≤ L. In other words, all the particles are initially in one half of the box.
(b) The final, steady-state solution of this problem corresponds to a uni- form density C = 1/2 throughout the box. Find the dominant long- time correction to this and use it to estimate the time required for the distribution to become uniform to within 1%.
Question 2 - 45 points
For an unbounded domain in 3D, the Green’s function G(r, r\ ) for L = −∇2 can only depend on the scalar separation |r, r\ |. This follows from isotropy and translation symmetry (again, in the absence of boundaries), but you may assume this. Thus, G reduces to a function of the scalar length r = |r| of a single vector r, i.e.,
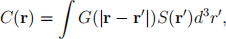
where the integral extends over all space where sources (S) are present. The defining equation for G
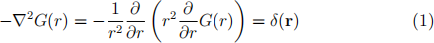
can be solved as follows.
(a) As in 1D, for any r ![]() 0, this equation can be written as a homogenous
0, this equation can be written as a homogenous
equation
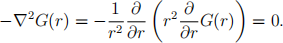
Demonstrate that G(r) = A/r is a solution to this for some constant A. What is the the form of the other homogenous solution, assuming a power-law form G(r) ∝ rm for some m? Explain why this must vanish since G(r) must vanish as r → ∞ in order to obtain physical, bounded solutions.
(b) The constant A can be obtained by integration of Eq. (1) above over all space (including r = 0). Since the δ-function above only contributes to the integral at r = 0, choose a sphere of radius R centered at the origin. (As in 1D, l δ(r)d3r = 1, provided that the integral includes r = 0.) Noting that −∇2 G(r) = −∇ · (∇(G(r))), convert the integral of this to a surface integral of ∇(G) over the sphere. (See, for instance, section A.5 or section 2.2 in Deen.)
(c) This approach can also be used for the diffusion problem with a first- order reaction (constant k):
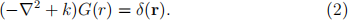
For this, it is convenient to consider an equivalent form of
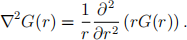
Solve for G(r). (Hint: multiply the homogeneous Eq. (2) for r > 0 by r to obtain a simpler equation for ϕ(r) = rG(r).) Assuming that G(r) vanishes as r → ∞, you should again have a single constant A to determine. You should be able to determine the unknown constant as in part (b), by considering a small but finite sphere radius R and estimating the contribution of the integral of kG for small R. Equiv- alently, you could also explain directly from Eq. (2) why G here must agree with that of part (b) in the limit r → 0+ .
2023-02-24