MATH0031 Exam 2021
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH0031
All questions should be attempted. Marks obtained in all solutions will count. The use of an electronic calculator is permitted in this examination.
NOTE: In the questions which follow the current price of an asset (or similar instrument) will often be denoted either by St or simply by S with the time subscript suppressed. Reference may be made to the following definitions:
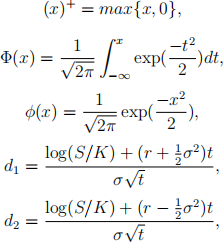
where K denotes the exercise price, r the riskless rate, σ the volatility and t is the time to expiry. The Black-Scholes formula for pricing a European call is
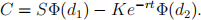
1. (a) Suppose GameStop shares satisfy the following one-period model:

WallStreetBetsTrader decides to buy GameStop shares at a price of $100 per share. She is concerned about the share price crashing and so to hedge her shares she also buys a put option on GameStop shares struck at K with expiration T where $25 < K < $400. Assuming the interest rate r = 0:
(i) Calculate the risk-neutral probability measure Q = (q1 , q2 ) corresponding to each of the outcomes in Ω .
(ii) Using the No-Arbitrage Theorem, determine whether there exists an arbitrage opportunity.
(iii) Let WallStreetBetsTrader’s portfolio be H(t, ωi ) for 0 < t < T . Calculate the gain or loss for this portfolio at time T for each ωi in terms of K.
(iv) Prove that the ratio of gains to losses for H(T, ωi ) is constant for all K . Express this ratio with respect to the probability measure Q. Give an intuitive explanation for why this ratio is constant.
(v) The financial regulator decides to ban short-selling in GameStop shares. What are the consequences for derivative traders in terms of replicating portfolios and market completeness?
(b) Using an arbitrage argument derive a relationship between the prices of an American call option and an American put option with the same strike K and ex- piration T on a stock with no dividends.
(c) Give an example of why you may choose to exercise an American option early.
2. (a) Consider a multi-period binomial model with T time-steps of length ∆t.
Derive the value of a put option struck at K in terms of the risk-neutral proba- bilities Q = (qU , qD ). You must give a clear definition for each variable required for this formula.
(b) Let C(K, t) be a European call option with strike K and expiration T. Using the binomial model with two time-steps, show by example how a trader constructs a self-financing trading strategy at each time-step to remain risk-neutral.
3. (a) An Asian option is a path-dependent option where the payoff is calculated using the average asset value for each path ω . So an Asian call option with strike price K has a payoff function given by,

where St (ω) denotes the asset price at time t for a given path ω . The asset S satisfies the following filtration (Pt )![]() , where r = 0 and the prices are in USD.
, where r = 0 and the prices are in USD.

(i) Define the conditional probability and the conditional expectation associated with Pt .
(ii) Calculate the conditional probabilities for each edge of the tree. Deduce the risk-neutral measure Q.
(iii) Show that for all paths ωi :
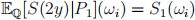
and
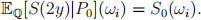
(iv) Hence or otherwise derive the value of a two year Asian call option with strike price K = $12 written on S .
(b) (i) Is the value of the Asian call option above greater or less than the value of a two year European call option with strike price K = $12? Justify your answer.
(ii) A Geometric Asian option calculates the geometric average price of the asset S to construct the payoff above. Is the Geometric Asian call option struck at K = $12 worth more or less than the Asian call option calculated in (a)(iv)? What about if they were puts instead of calls? Explain why.
4. (a) Let the process (B(t))t>0 be a standard Brownian motion and suppose c > 0 is a constant. Let τ be a stopping time such that B(τ ) = c and B(u) < c for all u < τ .
(i) Explain what is meant by saying τ is a stopping time.
(ii) Define
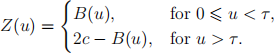
Describe the Brownian motion Z(u) in relation to B(t). Show that Z(u) is also a Brownian motion and calculate its mean and variance.
(b) W = W (t) is standard Brownian motion. Let f(S, t) be a function of two variables (continuously twice differentiable in S and once in t) obeying the stochastic differential equation:
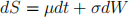
(i) Find an expression for
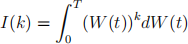
that does not involve Itˆo integrals.
(ii) Calculate the mean and variance of I(1). You may use without proof the fact that o[W (T)4] = 3T2 .
(iii) Evaluate

5. Let V (S, t) denote the value at time t ≤ T of a European option when the price of the underlying asset is S . Assume that the asset price process S(t) follows the stochastic equation

where W = W (t) is a standard Brownian motion, µ, σ are constants and r is a
constant riskless interest rate applicable throughout the life of the option. (a) Discuss market environments where the Black-Scholes model is less applicable.
(b) Suppose that S is a foreign exchange spot rate on USDJPY where USD has an interest rate given by rUSD and JPY has an interest rate given by rJPY . By hedg- ing the delta, derive a form of the Black-Scholes equation satisfied by the function V (S, t).
(c) A European binary call option with strike price K and expiration T has a payoff function given by

Using Feynman-Kac’s formula, solve the Black-Scholes equation in the case of a European binary call option.
2023-02-20