MATH0031 Exam 2019
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
MATH0031
All questions may be attempted but only marks obtained on the best four solutions will count.
The use of an electronic calculator is not permitted in this examination.
NOTE: In the questions which follow the current price of an asset (or similar instrument) will often be denoted either by St or simply by S with the time subscript suppressed. Reference may be made to the following definitions:
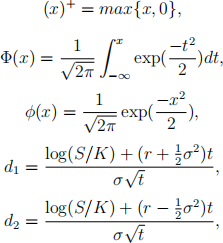
where K denotes the exercise price, r the riskless rate, σ the volatility and t is the time to expiry. The Black-Scholes formula for pricing a European call is
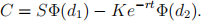
1. (a) Write-down the definitions of an arbitrage opportunity and a sure-thing arbi- trage. Using an arbitrage argument, show that American options must be worth at least as much as European options with the same strike and expiration.
(b) Assume we have a one-period model with no arbitrage opportunities. Prove that is is always possible to construct a risk-neutral measure Q.
(c) A European butterfly option has a payoff given by:
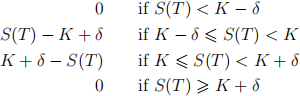
where S is the underlying asset price at time T, K is a strike price and 0 < 6 < K .
(i) Sketch the payoff diagram for a butterfly option.
(ii) Using put-call parity, show that the butterfly option can be constructed us- ing either a portfolio of call options or a portfolio of put options.
(d) Explain the differences between risk-neutral pricing and pricing based on the expected value of the underlying asset. If a hedge fund buys an option from a bank, how is it possible that they may both make money from the transaction?
2. (a) Consider the following model, where the interest rate r = 0:
S(t) is the asset price at time t in dollars.
(i) In this model, replicate the European call option with strike K = $101 over the two periods and so find the fair price of the option.
(ii) Find all the one period risk-neutral probabilities and the corresponding proba- bility on Ω = {ω1 , ω2 , ω3 , ω4 }. Confirm that EQ [X] is the fair price.
(iii) A trader sells 6 (six) European call options to a client for the option premium. For every path ωi explain how the trader creates a portfolio at each time step in order to deliver the option payoff to the client at expiration. Demonstrate that this trading strategy is self-financing.
(b) A one-period model where the initial stock price is S has equal probability of going up to SU or down to SD at time T where U = 1/D and U > 1.
Assuming rates are zero show that there must exist an arbitrage opportunity.
3. (a) (i) Let 伫 = (Pt )
be a filtration of Ω, and let H(0), . . . , H(T) be a sequence of random variables. Define what it means for H to be a previsible process.
(ii) If X is an adapted sequence of random variables, describe the condition required for X to be a martingale.
(iii) If X is a martingale and H is a bounded previsible process, prove that the gains process
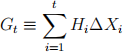
is a martingale.
(b) An Asian option is a path-dependent option where the payoff is calculated using the average asset value for each path ω . So an Asian call option with strike price K has a payoff function given by,
where St (ω) denotes the asset price at time t for a given path ω .
Derive the value of a two year Asian call option with strike price K = $2 written on an asset S with prices in dollars at each time and for each path given in the table below. Assume all interest rates are zero.
4. Write an essay on Itˆo calculus. You should:
(i) Derive Itˆo’s formula and show how this may be used to obtain a relationship between the standard (Riemann) integral and the stochastic integral.
(ii) Demonstrate by example that standard and stochastic integrals can lead to different results.
(iii) Describe the stochastic differential equation for a model for a stock and calculate the mean and variance for the stock from the model.
5. Let V (S, t) denote the value at time t ≤ T of a European option when the price of the underlying asset is S . Assume that the asset price process S(t) follows the stochastic equation
where W = W (t) is a standard Brownian motion, µ, σ are constants and r is a constant riskless interest rate applicable throughout the life of the option.
(a) State 5 assumptions of the Black-Scholes model.
(b) By hedging the delta derive the Black-Scholes equation satisfied by the function V (S, t), namely
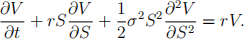
(c) A European binary call option with strike price K and expiration T has a
payoff function given by
Using Feynman-Kac’s formula, solve the Black-Scholes equation in the case of a European binary call option.
2023-02-20