CSOR 4231.001–Spring, 2023 Homework 1
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
CSOR 4231.001–Spring, 2023
Homework 1 (150 points)
Out: Monday, January 30, 2023
Due: 11:59pm, Monday, February 13, 2023
Homework Instructions.
1. For all algorithms that you are asked to “give” or “design”, you must do all of the following to get full credit:
(a) Describe your algorithm clearly in English.
(b) Give pseudocode.
(c) Argue correctness, even if you don’t give a formal proof and give a convincing argument instead.
(d) Give with an explanation the best upper bound that you can for the running time.
You are also encouraged to analyze the space required by your algorithm but we will not remove marks if you don’t, unless the problem explicitly asks you to analyze space complexity.
2. You should submit your assignment as a pdf file to Gradescope. Other file formats will not be graded, and will automatically receive a score of 0.
3. I recommend you type your solutions using LaTeX. For every assignment, you will earn 5 extra credit points if you type your solutions using LaTeX or other software that prints equations and algorithms neatly. If you do not type your solutions, make sure that your hand-writing is very clear and that your scan is high quality.
4. You should write up your solutions entirely on your own . Collaboration is limited to discussion of ideas only. You should adhere to the department’s academic honesty policy (see the course syllabus). Similarity between your solutions and solutions of your classmates or solutions posted online will result in receiving a 0 in this assignment, and possibly further disciplinary actions. There will be no exception to this policy and it may be applied retro- actively if we have reasons to re-evaluate your homework.

Figure 1: A tree corresponding to a comparison-based sorting algorithm on input x1 , x2 , x3 .
Homework Problems
1. (20 points) Consider the problem of computing N ! = 1 . 2 . 3 . . . N .
(a) (10 points) If N is an n-bit integer, how many bits long is N ! in Θ() notation? Give
your answer in terms of both of N, n.
(b) (10 points) Give an algorithm to compute N ! and analyze its running time. Give your
answer in terms of both of N, n. Assume that the time to multiply two n-bit integers is O(n2 ).
2. (40 points) On sorting
(a) (15 points) A lower bound for comparison- based sorting
You may view a comparison-based sorting algorithm as a binary tree. For example, the tree in Figure 1 sorts 3 integers x1 , x2 , x3 : it first compares x1 to x2 ; if x1 < x2 , it compares x2 to x3 , else is compares x1 to x3 , etc. Each leaf corresponds to a possible permutation of the 3 numbers. For example, if x1 < x2 < x3 , we get the leaf labelled x1 , x2 , x3 .
Suppose you want to sort n integers.
i. (2 points) Argue that every possible permutation of the n numbers must appear as a leaf in the tree corresponding to a sorting algorithm.
ii. (2 points) Fill in the missing number in the following sentence: Thus the tree has at least . . . leaves.
iii. (3 points) The worst-case time complexity of the sorting algorithm is given by the maximum number of comparisons performed by the algorithm. What does the latter quantity correspond to in the tree?
iv. (3 points) Consider a binary tree of depth d. Give with a proof an upper bound on the number of leaves of the tree.
v. (5 points) Derive a lower bound for the worst-case time complexity of a comparison- based sorting algorithm.
(b) (22 points) Give an algorithm that sorts any array of n integers x1 , . . . , xn in O(n + D) time, where D = max xi _ min xi . Hint: Think how to use extra space to achieve this
running time .
(c) (3 points) Suppose D is small (that is, O(n)). Does the algorithm you proposed in part (b) contradict the lower bound you derived in part (a)?
3. (30 points) The Hadamard matrices H0, H1 , H2 , . . . are defined as follows:
· H0 is the 1 × 1 matrix ┌ 1]
· For k > 0, Hk is the 2k × 2k matrix

Let ν be a column vector of length n = 2k . Can you compute the matrix-vector product Hkν faster than the straightforward algorithm that requires O(n2 ) time? (Assume that all the numbers involved are small enough that basic arithmetic operations like addition and multiplication take unit time.)
4. (60 points) The Fibonacci numbers are defined by the recurrence

(a) (4 points) Show that Fn ● 2n/2 , n ● 6.
(b) Assume that the cost of adding, subtracting, or multiplying two integers is O(1), inde-
pendent of the size of the integers.
i) (6 points) Give an algorithm that computes Fn based on the recursive definition above. Develop a recurrence for the running time of your algorithm and give an asymptotic lower bound for it.
ii) (8 points) Give a non-recursive algorithm that asymptotically performs fewer addi- tions than the recursive algorithm. Give an asymptotic upper bound for the new algorithm.
iii) (22 points) Give an algorithm to compute Fn in O(log n) time using only integer additions and multiplications.
(Hint: Observe that
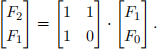
Can you build on this to compute Fn?)
· (20 points) Now assume that adding two m-bit integers requires Θ(m) time and
that multiplying two m-bit integers requires Θ(m2 ) time. What is the running time of the three algorithms in part (b) under this more reasonable cost measure for the elementary arithmetic operations?
RECOMMENDED EXERCISES: Do NOT submit, they will not be graded.
1. Give tight asymptotic bounds for the following recurrences.
![]() · T (n) = 4T (n/2) + n3 _ 1.
· T (n) = 4T (n/2) + n3 _ 1.
· T (n) = 8T (n/2) + n2 .
· T (n) = 6T (n/3) + n.
· T (n) = T (^n) + 1.
2. Show that, if λ is a positive real number, then f(n) = 1 + λ + λ2 + . . . + λn is
(a) Θ(1) if λ < 1.
(b) Θ(n) if λ = 1.
(c) Θ(λn ) if λ > 1.
Therefore, in big-Θ notation, the sum of a geometric series is simply the first term if the series is strictly decreasing, the last term if the series is strictly increasing, or the number of terms if the series is unchanging.
3. In the table below, indicate the relationship between functions f and g for each pair (f, g) by writing “yes” or “no” in each box. For example, if f = O(g) then write “yes” in the first box. Here logb x = (log2 x)b .
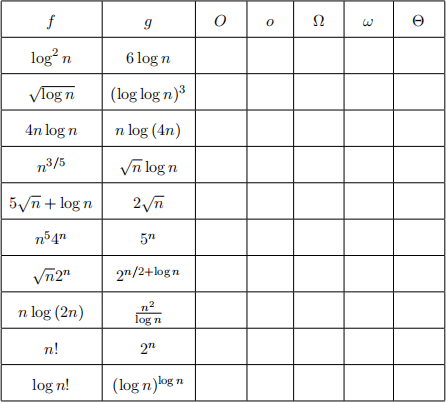
4. Give an efficient algorithm for the following problem: Input: A sorted array A of n distinct integers.
Output: An index i such that A[i] = i, if one exists; _1, otherwise.
5. An array A with n entries is said to have a majority element if more than half of its entries are the same. Given A, we want to find such a majority element, if one exists. A question of the form “Is A[i] = A[j]?” can be answered in constant time; however questions of the form “Is A[i] > A[j]?” are not permitted (for example, the elements of the array could be images so there is no order among them).
Give an algorithm to solve this problem in O(n log n) time.
2023-02-06