Some  of these problems  are  adapted from Dobrow.  For those problems,  the numbers refer to the problem numbers in the book.

1.  (1.22) Find E(Y |X) when (X,Y) is uniformly distributed on each of the following regions.

(a)  The rectangle [a,b] ⇥ [c,d].

(b)  The triangle with vertices (0, 0), (1, 0), (1, 1).

(c)  The disc with radius 1 centered at the origin.

2.  This question concerns Markov chain modelling of the game of snakes and ladders.  For the purposes of this assignment, the rules of snakes and ladders are as described on the last page of the assignment.

Consider the snakes-and-ladders board in Figure 1.

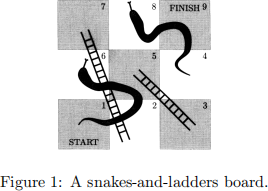
(a) Imagine a single player playing snakes-and-ladders on this board using a six-sided die. Give a transition matrix for a Markov chain with 5 states that models this.

(b) For the same  game as in question (a), give a transition matrix

for a 9-state Markov chain, with states 1, . . . , 9 representing the 9 squares of the board, for which it is possible to compute, e.g.,

P(T{3}  < T{5}), and more generally any probability of the form

P(TA  < TB|X0 = 1).

Here TA  = min(k : Xk  2 A) is the first hitting time of set A and A,B can be any subsets of {1, . . . , 9}.

(c)  Describe the state space and transition probabilities for a Markov chain modelling n-player snakes-and-ladders played on the board in Figure 1. Here n can be any positive integer.

3.  Recall the notation  [n] = {1, . . . ,n} from class.  Describe a Markov chain whose state space is the set of all subsets of [n], which models the evolution of the set of sampled integers when uniformly sampling without replacement from [n].

4.  (2.2) Let X0,X1 , . . . be a Markov chain on {1, 2, 3} with transition

matrix

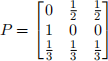
and initial distribution ↵ = ( , 0, ). Find the following:

(a) P(X2 = 1 | X1 = 3)

(b) P(X1 = 3,X2 = 1)

(c) P(X1 = 3 | X2 = 1)

(d) P(X9 = 1 | X1 = 3,X7 = 2)

5.  (Extension of 2.19) Let P be the transition matrix of a Markov chain with state space [k], and let I denote the k ⇥ k identity matrix.  Fix p 2 (0, 1) and let Q = pI + (1 − p)P.  Show that Q is a stochastic matrix, and give a probabilistic interpretation of the dynamics of a Markov chain with transition matrix Q, in terms of the dynamics of P.

6.  Show that the Markov chain with the transition graph shown in Fig- ure  2  can  not  be represented  as  a random walk on  an  undirected weighted graph.

(Recall that an undirected weighted graph is a graph G = (V,E) with undirected edges, together with non-negative edge weights (w(e),e 2 E).)

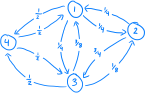
Figure 2: The transition graph of a Markov chain with state space {1, 2, 3, 4}.