Math 309: Introduction to knot theory Assignment 2
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Math 309: Introduction to knot theory
Assignment 2, due October 5 by 11:59 pm.
Exercises.
1. Prove that each of the 6-crossing knots in the knot table has unknotting number 1.
2. Find a family (cn : n e Z} such that cn is an oriented two component link whose linking number is n.
3. Define the “linking number of a knot” as follows: take a knot K, orient it, and assign +1 or _1 to each crossing, as in the definition of linking number; finally, take the sum of these +1s and _1s. Show that this procedure does not produce a knot invariant.
4. Based on material that we have seen so far in this course, show that the following links are non-trivial:
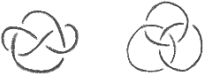
Problems.
5. Recall that McCoy’s theorem states that an alternating knot with unknotting number 1 admits an unknotting crossing in any minimal alternating diagram. Consider the following diagram then:
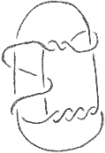
For this problem, let this represent a knot referred to as K .
(a) Show that, based on the diagram given, the unknotting number of K is at most 2.
(b) Find an alternating diagram for K, and using this give a proof that the unknotting number of K is exactly 2.
6. A simple link is a 2-component link with the property that if it can be isotoped so that there are exactly two crossings between the link components.
(a) Give an example, with proof, of a simple link. And, give an example, with proof, of a 2- component link that is not simple.
(b) Consider a simple link L with the property that each component is a 3-colourable knot. Prove that the link L is 3-colourable.
2023-01-14