Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit

Math 309: Introduction to knot theory

Assignment 1, due September 25 by 11:59 pm.

Exercises.

1. Recall, from class, that for a pair of relatively prime positive integers p and q we can form a knot with parametrization

y(t) = (2 + cos(pt)) cos(qt)

z(t) = (2 + cos(pt)) sin(qt)

-(t) = sin(pt)

where 0 ≤ t ≤ 2π .

(a) Consider the knot obtained in the case p = 2, q = 3, and consider the result of projecting this to the yz-plane and to the z--plane. Do both these projections give rise to knot diagrams? Why or why not?

(b) Find, with proof, values of p and q for which this paramatrization gives the knot 51 .

2. Figure 1.24 in ?1.3 of Adams depicts the following two distinct Reidemeister moves of type III:

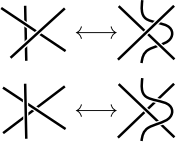
Using the Reidemeister moves of type I and II and the move (1), deduce the move (2).  (It is also possible to show that the move (1) follows from the type I and II moves together with (2)).

3. Links are introduced in Adams ?1.4. Show that the following diagrams describe the same link:

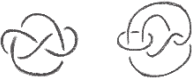
In your solution, explicitly identify where you made use of a Reidemeister Type III move.

4. Decide the 3-colourability of each of the knots 75 ,  76 ,  77 :  In each case,  either give a valid 3-colouring or prove that no 3-colouring exists.

Problems

5. The following infinite family of knots are referred to as twist knots:

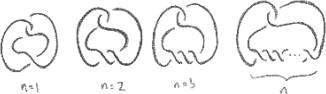
(a) Check that the case n = 1 is the knot 31 ; and that the case n = 4 is the knot 61 .

(b) Prove that a twist knot is 3-colourable if and only if n = 3k + 1.  (Recall that an if and only if statement requires that you check two implications!)

6. Using the notation from the table in Adams, the figure eight knot is the knot 4 1  and the trefoil knot is the knot 31 .

(a) A 5-colouring of a knot diagram is a choice of label from the set {0, 1, 2, 3, 4} (these are the five “colours”) for each of the strands so that at least two colours are used and at each crossing, if - is the label on the overstrand, the equation

y + z − 2- = 0 modulo 5

holds.  Show that the existence/non-existence of such a colouring is preserved under each of the Reidemeister moves.

(b) Show that the figure eight knot is 5-colourable.

(c) Using material that we have seen in the course and homework to this point, prove that the unknot, the trefoil, and the figure eight knot are mutually distinct.