MATH0034 Number Theory

Year:                                2021–2022

Code:                                MATH0034

Level:                                5 (UG)

Normal student group(s):     UG: Year 2 and 3 Mathematics degrees

Value:                                15 credits (= 7.5 ECTS credits)

Term:                                 2

Assessment:                        90% examination, 10% coursework

Normal pre-requisites:          MATH0006

Lecturer:                             Dr C Busuioc

Course Description and Objectives

This course is an introduction to elementary number theory. The main focus is on solving equations and congruences in integers, although various other rings will appear in the proofs of theorems.

Recommended Texts

(i) R. M. Hill, “Introduction to Number Theory”;

(ii) D. M. Burton, “Elementary Number Theory”;

(iii) W. Stein “Elementary Number Theory: Primes, Congruences, and secrets” (http://wstein.org/books/ent/);

(iv) H. Davenport, “The higher arithmetic” (this is mainly for the earlier parts of the course, and also for the final section on continued fractions);

Detailed Syllabus

The Euler totient function 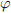. We’ll show how to calculate 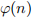. Using this, we’ll be able to calculate powers of integers modulo n, and solve congruences of the form 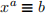mod n. 

Existence of primitive roots. In this section we’ll prove that for any prime number p, the multiplicative group 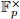 is cyclic.

Quadratic reciprocity. Given an integer a, we’ll answer the question: for which primes p is a a square modulo p?

Hensel’s Lemma. Suppose f is a polynomial, and we have a solution to f(x) ≡ 0 mod p. We’ll show how we can modify the solution to get a solution to f(x) ≡ 0 mod .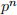

Power series modulo powers of primes. We’ll introduce the idea of a power series modulo 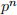. In particular introduce the logarithm and exponential functions on and prove their properties. We also decompose the group as a direct sum of the exponentials and the Teichm¨uller lifts. Introduction to the p-adic integers.

Factorization in quadratic rings. The Gaussian integers are numbers of the form x + iy where x and y are integers. These numbers form a ring, and this is an example of a quadratic ring. We’ll study quadratic rings in general, and prove that in a number of cases they have unique factorization. We’ll also show how to factorize a prime number in a quadratic ring, using the reciprocity law.

Continued fractions. We’ll describe the continued fraction expansion of a real number. As a consequence we’ll find a method for solving Pell’s equation 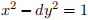. This allows us to find all the units in a real quadratic ring.

May 2021 MATH0034