MATH260001

Numerical Analysis

Calculator instructions:

• You are allowed to use a calculator which has had an approval sticker issued by the School of Mathematics.

Dictionaries:

• You are not allowed to use your own dictionary in this exam. A basic English dictionary is available to use: raise your hand and ask an invigilator, if you need it.

Exam information:

• There are 3 pages to this exam.

• There will be 2 hours to complete this exam.

• Answer all questions.

• All questions are worth equal marks.

• You must show all your calculations

1. (a) Show that the function f(x) = exp(x) − has only one zero, x∗. Write down the general step of Newton’s method for solving f(x) = 0. Starting with an initial guess of x0 = 0, calculate the next three approximations to the solution of f(x) = exp(x) −  = 0 using Newton’s method. For each iteration calculate the error from the exact solution.

Write down the map xn+1 = g(xn) corresponding to the Newton’s method solution of f(x) = exp(x) − = 0 and show that g'(x) = 0 at the fixed point. 

State the fixed point theorem giving the conditions that guarantee the iteration scheme xn+1 = g(xn) is stable and has a unique fixed point in the interval [a, b]. Show that g(x) satisfies the conditions of this theorem in a neighbourhood of x∗.

(b) Write down the Lagrange form of the interpolating polynomial P(x) that satisfies

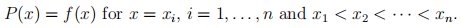
Find the form of the polynomial that interpolates f(x) =  through the points x1 = 0.5, x2 = 1 and x3 = 3, then simplify it. Use this polynomial to estimate the value of f(2) and find the error from the actual value.

Using the error formula for Lagrange interpolation,

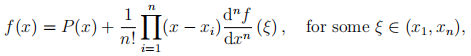
find upper and lower bounds for the error in your estimate above. How does this compare with the actual error?

2. (a) Simpson’s rule for integrating a function over the interval [−h, h] can be written in the form,

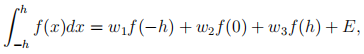
where w1, w2 and w3 are constants, and E represents the error term. Use the method of undetermined coefficients to find the constants w1, w2 and w3. Calculate the Simpson’s rule approximation to the integral

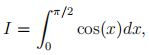
and calculate the error from the actual answer.

(b) Show that Simpson’s rule is exact for all cubic polynomials and hence using a suitable quartic polynomial obtain the error term in the form (where  denotes the fourth derivative of f) for some value  where K is a constant to be determined. Show that the error in the integral I is consistent with this error term.

3. (a) Consider the ordinary differential equation,

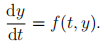
By integrating equation (5) over the interval  and approximating f(t, y) as a constant derive the forward Euler approximation,

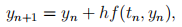
where (for all k).

Verify that y(t) = cos(t) is the solution of the initial value problem

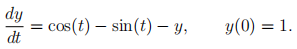
Use the forward Euler method to calculate an approximation to y(π/3) using a step-size of h = π/6 and calculate the absolute error from the exact solution y(π/3) = 0.5.

(b) By finding a suitable quadrature formula for integration of equation (5) over the interval derive the three-step Adams-Bashforth scheme,

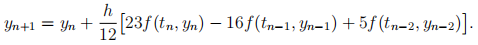
4. (a) Find the LU-factorisation of the matrix,

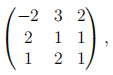
showing your method of working. Demonstrate how this factorisation may be used to solve the linear system,

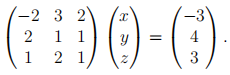
(b) Explain what is meant by (row) pivoting in the context of matrix factorisation. Show that the linear system,

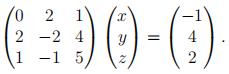
cannot be solved by LU-factorisation without pivoting even though the matrix is non-singular. Show how pivoting overcomes this problem and hence find the solution.