MATH10242

Two Hours

SEQUENCES AND SERIES

6 May 2018

1400–1600

Answer ALL SIX questions in Section A (40 marks in total.)

Answer TWO of the THREE questions in Section B (40 marks in total).

If more than TWO questions from Section B are attempted then credit will be given for the best TWO answers.

Electronic calculators are not permitted.

SECTION A

Answer ALL Six questions

A1. Define what is meant by a sequence 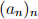being increasing and a sequence 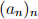being a strictly decreasing sequence. State the Monotone Convergence Theorem.

[4 marks]

A2. Fix 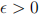. Find a natural number N such that

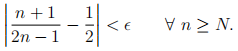
You should show your working.

[6 marks]

A3. Find the limits of the following sequences. You should show your working, but standard results from the course can be used without comment.

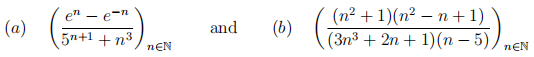
[6 marks]

A4. Using 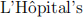Rule or otherwise, show that

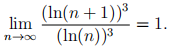
[5 marks]

A5. Determine whether the following series converge. In each case you should briefly justify your answer (in particular, saying what test you are using).

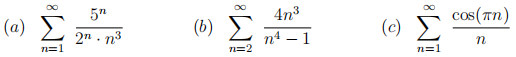
[12 marks]

A6. By quoting suitable tests, state why the series

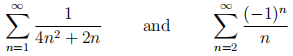
both converge. By using partial fractions, or otherwise, prove that their sums are equal.

[7 marks]

SECTION B

Answer TWO of the three questions

B7.

(i) What is meant by the statement that a sequence converges?

Suppose that is a null sequence and that is a bounded sequence. Prove that  is a null sequence. You must prove this from first principles, in particular using the definition of convergence.

(ii) Suppose that is a convergent sequence and that is a bounded sequence. Is it true in general that is a convergent sequence? You must justify your answer by either proving the result or giving a counterexample.

(iii) Prove that, for , where [−] denotes the integer part function.

(iv) Using subsequences, or otherwise, prove that the sequence does not converge.

[20 marks]

B8. Define a sequence 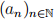inductively by

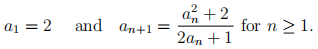
(a) Prove that is a decreasing sequence with for all .

(b) Prove that the sequence converges and find its limit.

(c) Define a sequence inductively by . Prove that the sequence does not converge.

You should state any results from the course that you use in the question. (The Algebra of Limits Theorem may be assumed without comment.)

[20 marks]

B9. Define what is meant by the radius of convergence of a power series .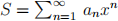

(i) Find the radius of convergence for the series .

(ii) Find the radius of convergence for the series .

(iii) Find the interval of convergence for the series .

In parts (i), (ii) and (iii) of this question, you should briefly justify your answers, in particular saying what tests you are using.

[20 marks]

END OF EXAMINATION PAPER