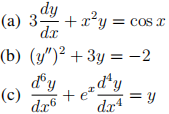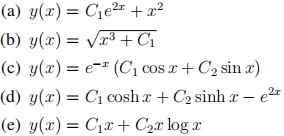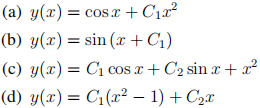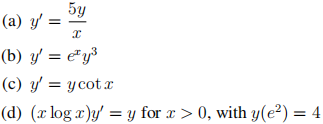MATH1400: Modelling with differential equations (Spring 2021) Examples 1
MATH1400: Modelling with differential equations (Spring 2021)
Examples 1
Section 1: to be covered in the tutorial. The solutions to some of these examples are given on the other side of this page.
1. For each of the following ordinary differential equations, state the order of the ODE, whether it is linear or nonlinear, and whether it is autonomous or non-autonomous.
2. Let C1 and C2 be arbitrary constants. For each of the following y(x), find a differential equation that y satisfies, with the order of the ODE equal to the number of arbitrary constants in y(x). The ODE should not contain any arbitrary constants. Hint: For the first-order examples, try to make combinations of y and y0 that eliminate C1. For the second-order examples, it may be necessary to try an ODE of the form y'' + Ay' + By = . . . (allowing A and B to be functions of x if needed).
3. Find the general solutions of the following separable ODEs, and then find the particular so-lution if an initial value is given. Wherever possible, write your solution y(x) as an explicit function of x. Verify that your solution is correct.
Section 2: to be handed in
Note that up to 3 marks (out of 20) are awarded for clarity and presentation. To gain these marks, show your working, structure your answers clearly and logically, and give appropriate explanations (using sentences as well as equations).
1. For each of the following ordinary differential equations, state the order of the ODE, whether it is linear or nonlinear, and whether it is autonomous or non-autonomous.
2. Let C1 and C2 be arbitrary constants. For each of the following y(x), find a differential equation that y satisfies, with the order of the ODE equal to the number of arbitrary constants in y(x). The ODE should not contain any arbitrary constants.
3. Find the general solutions of the following separable ODEs, and then find the particular so-lution if an initial value is given. Wherever possible, write your solution y(x) as an explicit function of x. Verify that your solution is correct.
Selected solutions to section 1.
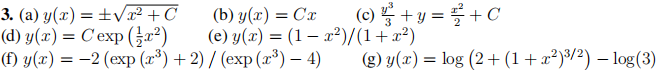
2021-05-14