MATH1400: Modelling with differential equations (Spring 2021)

Examples 5

Section 1: to be covered in tutorials.

1. The following differential equation is a model of an electric oscillator:

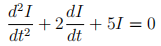
where I is the current in the oscillator and t is time. Find the general solution of this second-order linear constant coefficient homogeneous ODE. Describe what happens to this solution as t → ∞. If the oscillator is subjected to an imposed sinusoidal voltage source with frequency ω, the ODE that describes the situation is:

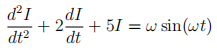
Find the general solution of this ODE. How does I(t) depend on ω in the limit t → ∞?

2. Find the general solution of the following two-dimensional systems of first-order ODEs by calcu-lating the eigenvalues and eigenvectors of the matrix. Identify and classify the fixed points. Sketch the phase portrait.

3. Convert the following ODEs into two-dimensional systems of first-order ODEs. Calculate the eigenvalues and eigenvectors of the appropriate matrix. Find the general solution if the eigenvalues are real. Identify and classify the fixed points. Sketch the phase portrait.

4. House buyers and sellers base their demand not only on the current selling price, but also on the rate of change of price (how quickly the price has been rising or falling), and possibly also on whether this rate of change is slowing down or speeding up (the second derivative of price). Suppose that the demand for houses, D(t), is given by:

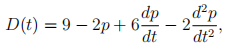
where p(t) is the price. Note that demand goes down when the price is higher (−2p), that demand increases if prices are rising (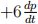, buy now before it is too late!), and that demand decreases if the rate of price increase is itself increasing ().

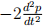Suppose also that the supply of houses, S(t), on the market is given by:

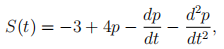
Note the signs are mainly opposite to those in the expression for demand.

By assuming that the market is in equilibrium, that is, assuming that the supply equals demand, obtain a second-order linear ODE for the market price, p(t). Convert this into a two-dimensional system of first-order ODEs. Identity the fixed points and find the general solution by calculating the eigenvalues and eigenvectors of the appropriate matrix. Classify the fixed points and sketch the phase portrait. What does this model tell you about house prices? Is it a sensible model? (This example is from Mathematics for economics and finance: methods and modelling, by Martin Anthony and Norman Biggs, CUP 1996.)

Section 2: to be handed in.

1. Consider the following two-dimensional system of first-order ODEs:

(a) Find the general solution by calculating the eigenvalues and eigenvectors of the matrix.

(b) Identify and classify the fixed points. Sketch the phase portrait.

2. Consider the following second-order ODE:

(a) Let . Convert the above ODE into a two-dimensional system of first-order ODEs with x and y as the dependent variables. Identify the fixed points.

(b) Calculate the eigenvalues of the appropriate matrix and classify the fixed points. 

(c) Find the equation of the trajectories on the xy-plane. Sketch the phase portrait.

3. Consider the following ODE that describes the current I in an RLC oscillator with no voltage source:

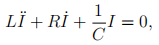
where the positive constants L, R and C are the inductance, resistance and capacitance respec-tively. (There can be current in the circuit even when there is no voltage source because there could be initially some charge in the capacitor.)

(a) Let . Convert the given ODE into a two-dimensional system of first-order ODEs with I and J as the dependent variables. Identify the fixed points.

(b) If , classify the fixed point by calculating the eigenvalues of the appropriate matrix. Is the oscillator overdamped, critically damped or underdamped?

(c) If , classify the fixed point. Is the oscillator overdamped, critically damped or underdamped?