MAT202H5F - Discrete Math

Fall 2020

Final Exam

Instructions

● Before starting, please make sure you have logged in and signed the academic integrity dec-laration at http://mcs.utm.utoronto.ca/declaration.

● This test consists of 6 questions. You must upload solutions to each question individually on Crowdmark.

● Solutions must be uploaded by 4:00PM EST. Any submission that is late by even one minute will not be marked. You must start uploading by 3:30PM EST.

● You may either use LATEX to type up your solutions or hand-write them on paper (and take a picture/scan), or write them digitally on a tablet.

● Aids allowed: Scientific calculator, course notes, your notes, our Quercus page and anything linked from it, and online calculators like WolframAlpha.

● You are expected to do the work independently. This means that you are not allowed to communicate in person or digitally with any other individual about the test (except for the instructor and TAs). Any solutions you submit should be your own work.

You are expected to write-up your solutions with clear and complete explanations, using English words as well as mathematics.

Solutions with no explanations or with just the final answer will get zero for that question.

(Q1) Consider the word TORTOISE. Count the number of arrangements of this word

(a) such that no two vowels are beside each other. [4]

(b) that satisfy: [4]

● vowels are not in alphabetical order left-to-right, and

● consonants are not in alphabetical order left-to-right.

Note: Vowels are allowed to be beside each other. For example, the word TEISROTO is invalid, because its vowels EIOO are in alphabetical order left-to-right. But the word TOESROTI is valid.

(Q2) Let a, b, c, n 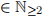with n = a + b + c. Prove without using algebra that [6]

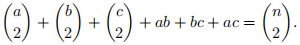
(Q3) (a) Show that 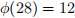by listing all integers in {1, 2, . . . , 28} relatively prime with 28. [2]

(b) Citing a theorem from the course notes, explain how we know that 5¹¹ is an inverse of 5 modulo 28. Then use an online calculator to compute the remainder when 5¹¹ is divided by 28. [3]

(Note: Indicate which software/website you used to compute this remainder, or attach a screenshot of the calculation.)

(c) Use your result in (b) to solve the congruence [3]

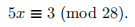
(Q4) Let n, k N, and define the family of graphs 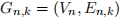on the vertex set

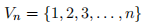
and with edge set

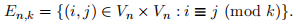
In other words, two vertices i and j are adjacent if they are congruent modulo k.

(a) Draw 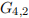and and show they are both disconnected. [2]

(b) Show that 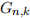is connected if and only if k = 1. [4]

(c) Show that 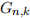is the empty graph if and only if n ≤ k. [4]

(Q5) Draw a simple graph (or argue why one cannot exist) that

(a) has 6 vertices, 12 edges, and is disconnected. [3]

(b) is Eulerian, is bipartite, and is Hamiltonian. [3]

(c) has 7 vertices, is acyclic, connected, and has 6 vertices of degree 2. [3]

(d) has average degree 3, but has no C3 subgraph. [3]

Note: these are all separate sets of conditions. If you give an example, make sure you justify/explain why that example works.

(Q6) (a) Suppose G = (V, E) is a connected simple graph, and let x, y V be two vertices in G. Show that if there are three distinct (not necessarily disjoint) paths from x to y in G, then G has at least two cycle subgraphs. [4]

Note: You may use any result in the course notes and assignments without proof. If necessary, you may also use the fact that in a tree there is always a unique path between any two vertices.

(b) Show that G may not necessarily have three cycle subgraphs by giving an example of a graph G, and vertices x and y of G, so that there are at least three distinct x-y paths but G only has two cycle subgraphs. Label the vertices of G and give the paths explicitly. [2]

End of Final Exam