MENG10004 Engineering Science 2022/2023
Hello, dear friend, you can consult us at any time if you have any questions, add WeChat: daixieit
Engineering Science (MENG10004)
Mechanics : Statics, Kinematics, Dynamics
2022/2023
Handout 8 – Linear Momentum, Impact and Rockets
|
Meriam & Kraige, Dynamics: 3/9, 3/12, 4/4-4/7, 6/8 |
In the previous handout, the concepts of work and energy were introduced to dynamics. These are integrals of the dynamic forces with respect to displacement, and applying the work-energy equations avoided having to find accelerations in order to determine velocities. Similarly, the dynamic forces can be integrated with respect to time, leading to impulse and momentum formulations. The conservation of momentum can be used to simplify the analysis of dynamics problems and offer elegant new insights.
8.1 Linear Momentum of Particles
Consider the planar motion of a particle of mass m, under applied net force F .

A net force F on the particle will result in an acceleration a along the direction of the force vector.
 (8.1)
(8.1)
where
p = mv (8.2)
is defined as the linear momentum of the particle; it is a vector quantity with units Ns. In other words, the time derivative of the momentum vector p is equal to the force F applied to the particle. Note that the force (acceleration) and momentum (velocity) vectors will generally not be aligned!
The time integral of the applied force f is known as the linear impulse:
 (8.3)
(8.3)
and is equal to the change in linear momentum ∆p; this may involve changes in both magnitude and direction of the linear momentum. Thus, if no net external force is applied, the linear momentum must be conserved.
Example 8.1 – Cannon Recoil
Consider the recoil of a ship’s cannon that fires a projectile. Let the gun be at rest, the bore aimed horizontally and the gun allowed to roll freely. As the explosive charge fires, it exerts a force on both the gun and the projectile (and thus imparts an equal and opposite impulse).

The momentum of the combined system must therefore remain constant:
∆p = pp + pc = mp vp { mc vc = 0
Where pp and pc are the momentum of the projectile and cannon, respectively. Therefore, the velocities of the cannon and the projectile will be inversely proportional to their mass:

Now consider the kinetic energy of both the projectile and the cannon. These are scalar quantities, and the energy of both need to be added up to obtain the total energy of the system.
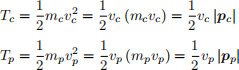
The linear momentum of both is equal, and therefore the kinetic energy will be in ratio of the velocities, and therefore in inverse ratio of mass. This means that the kinetic energy of the projectile will be much greater than that of the cannon. (Which is the purpose of a cannon ball!)
Q: Why is the momentum of the cannon and projectile the same, but their kinetic energy different?
Example 8.2 – Sliding Ladder
Consider a ladder standing on a smooth surface and leaning against a frictionless wall. Due to the absence of friction, the ladder will slide down and gain a horizontal, vertical and angular velocity.

The work done by the weight mg increases the kinetic energy as the ladder slides down, and although the reaction forces do no work, they impart a linear impulse: the horizontal reaction force results in a horizontal velocity of the ladder!
Example 8.3 – Aircraft Lift
Aircraft lift — or, how does a plane stay in the sky? — can in part be explained by the change in momentum of the incoming air flow, which is diverted downward by the wing. The lift force L is the vertical component of R = dp/dt.

8.2 Momentum: System of Particles
Consider a system of n particles, each described by position vector ri , and linear momentum pi . Let fij be
the internal force exerted by particle j on particle i, and Fi the external force applied to particle i.

The total linear momentum of the system is the vector sum of the momentum of the individual particles:

The time derivative of the linear momentum pi equals the net force on the particle (Newton’s 2nd Law):

For the total system of particles all internal forces will cancel out (Newton’s 3rd Law):

Thus, if all external forces are zero, the total momentum of the system of particles will be conserved, regardless of the internal interactions between the particles.
The total linear momentum of the system of particles can be rewritten as

where m is the total mass, and UG is the velocity of the centre of mass of the system. In general, in absence of external forces the velocity of the centre of mass of an enclosed system of particles will be constant, regardless of the interactions between the particles.
This remarkable result has elegant consequences! For the example of the cannon and the projectile, the centre of mass will remain stationary as the combined system started from rest. In a fireworks display, after the rocket explodes into its colourful pattern, the centre of mass will continue to describe a parabola, as if it were a single particle. At a larger scale, the combined centre of mass of the solar system will move irrespective of the internal gravitational forces between the sun, planets and other objects.
Example 8.4 – Two Masses and a Spring
Two masses, m1 = 1 kg and m2 = 2 kg, are connected by a spring with stiffness of k = 5 N/m with a rest length of Ld = 1 m, and m2 is given an initial horizontal velocity vd = 2 m/s. As illustrated by the simulation results, the centre of mass travels uniformly while the two masses move seemingly erratically as a result of the varying spring force.

8.2.1 Linear Momentum of Rigid Body
Clearly, the previous discussion applies to a rigid body, which can be regarded as a system of particles where the internal stresses maintain the geometry. Therefore, the linear momentum of a rigid body is:
p = mvG (8.4)
and
 (8.5)
(8.5)
where the net force F on the body determines the acceleration of its centre of mass.
This analysis supports the assertion made in Handout 5 that the general motion of a rigid body can be described by the acceleration of its centre of mass, and the angular acceleration of the rigid body around the centre of mass. This will be elaborated on further in Handout 9, when studying angular momentum.
8.3 Impact of Particles
A collision between two particles, or impact, results in a relatively large contact force acting over a very short period of time. Such an impact involves material deformation (elastic and plastic), as well as dissipation of energy through the generation of heat and sound. The precise force-time relationship is complex, but is not required to determine the total impulse involved during the impact.
8.3.1 Direct Central Impact
Consider two particles with mass m1 and m2 during the three stages of collinear impact: (a) before impact the particles have velocities v1 and v2 , with v1 > v2 ; (b) during impact both particles momentarily assume identical velocity v; (c) after impact the particles have velocities v ![]() and v
and v![]() . It is assumed that only the large contact forces are significant for the calculations, and that the particles remain rigid (i.e. no change in position of centres of mass during impact).
. It is assumed that only the large contact forces are significant for the calculations, and that the particles remain rigid (i.e. no change in position of centres of mass during impact).

conservation of momentum: the contact forces during impact are equal and opposite, so the combined linear momentum of the two colliding particles must be conserved. Therefore:
m1 v1 + m2 v2 = m1 v ![]() + m2 v
+ m2 v![]() (8.6)
(8.6)
As only a single equation describes the two velocities v ![]() and v
and v![]() after impact, a unique solution cannot be found from momentum considerations alone.
after impact, a unique solution cannot be found from momentum considerations alone.
coefficient of restitution: the ratio between the relative velocities before and after impact follows from an energy argument, and is defined by the coefficient of restitution:
 (8.7)
(8.7)
where e 2 [0, 1]. For e = 1 all kinetic energy is conserved.
It is therefore tempting — but incorrect! — to speculate that the coefficient of restitution is the ratio of the kinetic energy after/before collision. A more detailed analysis of the impact reveals that:

where Ebc and Eab are the kinetic energy gained and lost in the two stages of the impact (stored in and released from elastic deformations), and Ibc and Iab are the impulse imparted.
The coefficient of restitution enables impact calculations, but also obscures details such as the precise contact forces. Its value depends on the material properties as well as the velocity of impact and is generally determined experimentally.
Using these two equations, combining momentum and energy considerations, the velocities of the particles after impact can be found. We first consider two special cases, that of purely elastic and purely inelastic impact, before describing general impact.
purely elastic impact: all kinetic energy is conserved, with coefficient of restitution e = 1, resulting in the following velocities after impact:

For the special case of equal masses, m1 = m2 , this becomes:
v ![]() = v2 v
= v2 v![]() = v1
= v1
and therefore the velocities of the particles are exchanged.
This is elegantly demonstrated with the “Newton’s Cradle” toy where a stationary ball is struck by a moving ball of equal mass, which then assumes the same velocity.
Example 8.5 – Impact with Flat Wall
Consider the limit case of an elastic collision between a particle and a large flat body.

In that case, v2 = 0, while m2 can be considered infinite. This gives:

The result offers no surprises, with the ball bouncing back at the same velocity as it struck the wall.
Note that the linear momentum of the particle changed as a result of reversing its velocity
∆p1 = {2m1 v1
and the required impulse was provided by the stationary wall. The precise contact force and contact time of the collision become irrelevant to the calculations, by considering the total impulse.
purely inelastic impact: in a purely inelastic collision, with coefficient of restitution e = 0, the particles have the same velocity v\ after impact.
![]() m1 v1 + m2 v2
m1 v1 + m2 v2
Although momentum is conserved, the kinetic energy after impact is reduced:
∆T = ![]() m1 v 1(2) +
m1 v 1(2) + ![]() m2 v2(2) {
m2 v2(2) { ![]() (m1 + m2 ) ╱
(m1 + m2 ) ╱ ![]() 、2
、2
= ![]()
![]() (v1 { v2 )2
(v1 { v2 )2
In fact, all kinetic energy can disappear during a collision! (When is this the case?)
Example 8.6 – Ballistic Pendulum
A ballistic pendulum is an effective method to measure the velocity of a projectile, without the need for high-speed cameras. It consists of a bifilar pendulum of length L that supports a sand box of mass M . The projectile is fired into the sand box, and its velocity can be determined from the maximum deflection angle θ .
![]()
 θ
θ
L
![]()
![]() v0
v0 ![]()
![]() Δ h
Δ h
M
From conservation of linear momentum:
mvd = (M + m)v\
the velocity v\ of the sand box and projectile directly after impact is found.
The maximum deflection angle θ is subsequently found through the conservation of energy; at the maximum deflection the velocity, and therefore kinetic energy, will be zero. The work-energy balance:
∆T+ ∆V = 0
┌0 { ![]() (M + m) v\2┐ + [(M + m) g∆h { 0] = 0
(M + m) v\2┐ + [(M + m) g∆h { 0] = 0
where
∆h = L (1 { cos θ)
gives
θ = arccos ╱ 1 { ╱ ![]() 、2
、2 ![]() \
\![]()
general impact In general, impact between particles will be partially elastic, as defined by the coefficient of restitution e, where 0 < e < 1. From the conservation of momentum and the coefficient of restitution, the velocities after impact are determined as:
![]() m1 v1 + m2 v2 { e m2 (v1 { v2 )
m1 v1 + m2 v2 { e m2 (v1 { v2 )
m1 + m2
m1 v1 + m2 v2 { e m1 (v2 { v1 )
m1 + m2
The loss of kinetic energy over the impact can be calculated, and (after some algebra) reduces to:
∆T = ![]()
![]() (v1 { v2 )2
(v1 { v2 )2
Example 8.7 – Two-Ball Bounce
In the classic two-ball bounce experiment a tennis ball is placed on top of a basket ball, and both are dropped simultaneously.

Q: How high will the balls bounce after impact with the ground?
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



![]()

![]()

![]()

![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
It is assumed that the mass of the basket ball is much greater than that of the tennis ball (m2 >> m1 ), and a small (assumed) separation between the balls ensures that the impact can be modelled as two independent collisions: first, the basket ball hits the ground, bounces back, and then strikes the tennis ball. The coefficient of restitution between the balls is e12 and between the basket ball and the ground e2 .
g
![]() impact between balls
impact between balls
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 1
1
![]()
![]()
![]()
![]()
![]() 2
2
From potential energy, we find velocity vd of both balls at time of impact with the ground: vd = {^2g (y2 { r2 )
After impact the upward velocity of the basket ball becomes:
v![]() = {e2 vd
= {e2 vd
Next, the two balls travelling at v1 and v2 collide, giving the following velocities after impact:
![]() µv1 + v2 { e12 (v1 { v2 )
µv1 + v2 { e12 (v1 { v2 )
µ + 1
µv1 + v2 { e12 µ (v2 { v1 )
µ + 1
where µ = m1 /m2 . For the case of zero initial separation, substitute v2 年 v![]() = {e2 vd and v1 年 vd to find:
= {e2 vd and v1 年 vd to find:
![]() µ { e2 { e12 (1 + e2 )
µ { e2 { e12 (1 + e2 )
µ + 1
![]() µ { e2 + µe12 (1 + e2 )
µ { e2 + µe12 (1 + e2 )
µ + 1
Taking the limit of the mass ratio µ = m1 /m2 年 0
v ![]() 年 { [e2 + (1 + e2 ) e12 ] vd
年 { [e2 + (1 + e2 ) e12 ] vd
v![]() 年 {e2 vd
年 {e2 vd
and assuming purely elastic collisions, e2 = e12 = 1, this reduces to
v ![]() 年 {3vd
年 {3vd
v![]() 年 {vd
年 {vd
which means that the resulting velocity of the tennis ball can be up to 3 times its initial velocity. This means its kinetic energy will be 9 times greater, and thus launch 9 times higher than it started!
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
8.3.2 Oblique Central Impact
The methods described for direct central impact can be extended to a case where the intial and final velocities are not collinear. Consider two colliding particles of mass m1 and m2 and initial velocities U1 and U2 .
![]() n v’ 1
n v’ 1
![]()

![]() 1
1
![]()
![]()
![]()
![]()
![]()
![]() θ 1
θ 1
θ2
![]() 2
2
![]()
![]()
F
-F
![]()
![]()
The directions of the velocity vectors are measured in an nt-coordinate system, which is defined by axes normal and tangent to the contact point. It is assumed that the equal and opposite contact forces during impact only act in the n direction. Four equations are needed to solve for the velocity vectors after impact:
❼ conservation of momentum in n-direction:
m1 v1n + m2 v2n = m1 v ![]() n + m2 v
n + m2 v![]() n
n
❼ conservation of momentum in t-direction for both particles; as no impulse is applied: m1 v1t = m1 v ![]() t
t
m2 v2t = m2 v![]() t
t
❼ coefficient of restitution in n-direction:
e = v![]() n { v
n { v ![]() n
n
v1n { v2n
These equations are solved simultaneously to find the components of the velocity vectors U ![]() and U
and U![]() .
.
2023-05-26
Mechanics : Statics, Kinematics, Dynamics